题目内容
15．
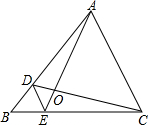如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S△BDE：S△CDE=1：3，则S△DOE：S△AOC的值为1：16．
分析 证明BE：EC=1：3，得出BE：BC=1：4；证明△DOE∽△AOC，得到$\frac{DE}{AC}=\frac{BE}{BC}$=$\frac{1}{4}$，由相似三角形的性质即可解决问题．
解答 解：∵S△BDE：S△CDE=1：3，
∴BE：EC=1：3；
∴BE：BC=1：4；
∵DE∥AC，
∴△DOE∽△AOC，
∴$\frac{DE}{AC}=\frac{BE}{BC}$=$\frac{1}{4}$，
∴S△DOE：S△AOC=（$\frac{DE}{AC}$）2=$\frac{1}{16}$；
故答案为：1：16．
点评 本题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是灵活运用形似三角形的判定及其性质来分析、判断、推理或解答．
练习册系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
5．
如图，已知∠AOB=30°，M为OB上一点，且OM=5cm，以M为圆心，以r为半径作圆，则当r=4cm时，⊙M与直线OA的位置关系是（ ）
如图，已知∠AOB=30°，M为OB上一点，且OM=5cm，以M为圆心，以r为半径作圆，则当r=4cm时，⊙M与直线OA的位置关系是（ ）| A． | 相交 | B． | 相切 | C． | 相离 | D． | 都有可能 |
如图，已知抛物线y=-x2+2x+3与x轴交于A、B两点，A点在B点左侧，与y轴交于点C．P为BC上的一个动点，过P作BC的垂线交抛物线于M、N两点．若四边形BMCN的面积为12，求直线MN的解析式．
7．
这是一根起点为0的数轴，现有同学将它弯折，如图所示，例如：虚线上第一行0，第二行6，第三行21…，第4行的数是（ ）
这是一根起点为0的数轴，现有同学将它弯折，如图所示，例如：虚线上第一行0，第二行6，第三行21…，第4行的数是（ ）| A． | 45 | B． | 54 | C． | 46 | D． | 55 |