题目内容
5.解方程组:$\left\{\begin{array}{l}{\frac{6}{x}+\frac{6}{y}=1}\\{\frac{10}{y}+\frac{10}{z}=1}\\{\frac{5}{x}+\frac{5}{z}=\frac{2}{3}}\end{array}\right.$.分析 设a=$\frac{1}{x}$,b=$\frac{1}{y}$,c=$\frac{1}{z}$,把原方程组转化为三元一次方程组求得a、b、c进一步求得原方程组的解即可.
解答 解:设a=$\frac{1}{x}$,b=$\frac{1}{y}$,c=$\frac{1}{z}$,则原方程为
$\left\{\begin{array}{l}{6a+6b=1}\\{10b+10c=1}\\{5a+5c=\frac{2}{3}}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=\frac{1}{10}}\\{b=\frac{1}{30}}\\{c=\frac{1}{15}}\end{array}\right.$,
则x=10,y=30,z=15,
所以原方程组的解为$\left\{\begin{array}{l}{x=10}\\{y=30}\\{z=15}\end{array}\right.$.
点评 此题考查解三元一次方程组,掌握解三元一次方程组的方法与步骤是解决问题的关键.

练习册系列答案
相关题目
13.下列条件中,能作出唯一的三角形的条件是( )
| A. | 已知三边作三角形 | |
| B. | 已知两边及一角作三角形 | |
| C. | 已知两角及一边作三角形 | |
| D. | 已知一锐角和一直角边作直角三角形 |
17.如果两个有理数的和除以它们的积,所得的商为0,那么这两个有理数( )
| A. | 互为倒数 | B. | 互为相反数但均不为0 | ||
| C. | 有一个数为0 | D. | 都等于0 |
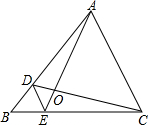 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为1:16.
如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为1:16.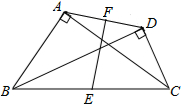 已知:如图,∠BAC=∠BDC=90°,点E在BC上,点F在AD上,BE=EC,AF=FD.求证:EF⊥AD.
已知:如图,∠BAC=∠BDC=90°,点E在BC上,点F在AD上,BE=EC,AF=FD.求证:EF⊥AD. 如图,将一副三角板叠放在一起,使直角顶点重合于O点.
如图,将一副三角板叠放在一起,使直角顶点重合于O点.