题目内容
4.如果分式$\frac{2}{x-1}$与$\frac{3}{x+3}$的值互为相反数,那么x的值是$-\frac{3}{5}$.分析 根据互为相反数的性质,相加得0,列出分式方程,根据解分式方程的一般步骤,直接解方程即可.
解答 解:根据题意,得:$\frac{2}{x-1}+\frac{3}{x+3}=0$,
两边同乘(x-1)(x+3),得:2(x+3)+3(x-1)=0,
解得:x=$-\frac{3}{5}$,
检验:当x=$-\frac{3}{5}$时,最简公分母(x-1)(x+3)≠0,
∴x=$-\frac{3}{5}$是所列分式方程的解,
故答案为:$-\frac{3}{5}$.
点评 本题主要考查解分式方程.根据题意列出分式方程时解决此题的关键,此外,在解分式方程时一定要进行检验.

练习册系列答案
相关题目
13.下列条件中,能作出唯一的三角形的条件是( )
| A. | 已知三边作三角形 | |
| B. | 已知两边及一角作三角形 | |
| C. | 已知两角及一边作三角形 | |
| D. | 已知一锐角和一直角边作直角三角形 |
 (1)求对称轴是x=-2,且开口方向、形状都与y=2x2相同,还过原点的抛物线的解析式.
(1)求对称轴是x=-2,且开口方向、形状都与y=2x2相同,还过原点的抛物线的解析式.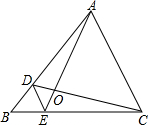 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为1:16.
如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为1:16. 如图,已知A,O,E三点在同一条直线上,OB平分∠AOC,OD平分∠COE,则∠BOC与∠COD的关系为∠BOC+∠DOC=90°.
如图,已知A,O,E三点在同一条直线上,OB平分∠AOC,OD平分∠COE,则∠BOC与∠COD的关系为∠BOC+∠DOC=90°. 如图,抛物线y=(x+2)2-9与x轴交于点A、B(点A在点B的左边).
如图,抛物线y=(x+2)2-9与x轴交于点A、B(点A在点B的左边).