题目内容
6．计算$\frac{\sqrt{8}}{\sqrt{2a}}$=（ ）| A． | $\frac{2\sqrt{a}}{a}$ | B． | 2$\sqrt{a}$ | C． | 4$\sqrt{a}$ | D． | 2a |
分析 直接利用二次根式的乘除运算的性质化简求出答案．
解答 解：$\frac{\sqrt{8}}{\sqrt{2a}}$=$\frac{2\sqrt{2}}{\sqrt{2}×\sqrt{a}}$=$\frac{2\sqrt{a}}{a}$．
故选：A．
点评 此题主要考查了二次根式的除法运算，正确化简二次根式是解题关键．
练习册系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
16．在平面直角坐标系中，点（a-3，2a+1）在第二象限内，则a的取值范围是（ ）
| A． | -3＜a＜$\frac{1}{2}$ | B． | $\frac{1}{2}$＜a＜3 | C． | -3＜a＜-$\frac{1}{2}$ | D． | $-\frac{1}{2}$＜a＜3 |
1．
如图，在直角坐标系中，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时，反射角等于入射角，当小球第1次碰到矩形的边时的点为P1，第2次碰到矩形的边时的点为P2，…，第n次碰到矩形的边时的点为Pn，则点P2016的坐标是（ ）
如图，在直角坐标系中，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时，反射角等于入射角，当小球第1次碰到矩形的边时的点为P1，第2次碰到矩形的边时的点为P2，…，第n次碰到矩形的边时的点为Pn，则点P2016的坐标是（ ）| A． | （0，3） | B． | （5，0） | C． | （0，5） | D． | （7，4） |
18．
如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒$\frac{π}{2}$个单位长度，则第2017秒时，点P的坐标是（ ）
如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒$\frac{π}{2}$个单位长度，则第2017秒时，点P的坐标是（ ）| A． | （2016，0） | B． | （2017，1） | C． | （2017，-1） | D． | （2018，0） |
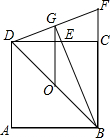如图，O是正方形ABCD的中心，BE平分∠DBC，交DC于点E，将点E绕着点C按顺时针方向旋转90°得到点F，连接CF，DF，BE的延长线交DF于点G，连接OG．
如图，将矩形ABCD沿对角线BD所在直线折叠，点C落在同一平面内，落点记为C′，BC′与AD交于点E，若AB=3，BC=4，则DE的长为$\frac{25}{8}$．