题目内容
4.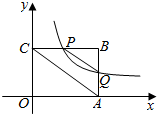 如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,点B的坐标为(4,3),双曲线y=$\frac{k}{x}$(x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q
如图,平面直角坐标系中,矩形OABC的一边OA在x轴上,点B的坐标为(4,3),双曲线y=$\frac{k}{x}$(x>0)交线段BC于点P(不与端点B、C重合),交线段AB于点Q(1)若P为边BC的中点,求双曲线的函数表达式及点Q的坐标;
(2)求k的取值范围;
(3)连接PQ,AC,判断:PQ∥AC是否总成立?并说明理由.
分析 (1)先求出点P坐标,再利用待定系数法求出反比例函数解析式,根据点Q的横坐标即可求出点Q的纵坐标.
(2)设点P(x,3),则x=$\frac{k}{3}$,列出不等式即可解决问题.
(3)根据两边成比例夹角相等的两个三角形相似证明△BPQ∽△BCA,即可解决问题.
解答 解:(1)∵四边形OABC是矩形,
∴BC∥OA,
∵点B坐标(4,3),
∴BC=4,AB=3,
∵PC=PB,
∴点P坐标(2,3),
∴反比例函数解析式y=$\frac{6}{x}$,
∵点Q的横坐标为4,
∴点Q的坐标为(4,$\frac{3}{2}$).
(2)设点P坐标(x,3),则0<x<4,
把点P(x,3)代入y=$\frac{k}{x}$得到,x=$\frac{k}{3}$,
∴0<$\frac{k}{3}$<4,
∴0<k<12.
(3)结论:PQ∥AC总成立.
理由:设P(m,3),Q(4,n),则3m=4n=k,
∴$\frac{BP}{BC}$=$\frac{4-m}{4}$=$\frac{4-\frac{k}{3}}{4}$=$\frac{12-k}{12}$,
$\frac{BQ}{BA}$=$\frac{3-n}{3}$=$\frac{3-\frac{k}{4}}{3}$=$\frac{12-k}{12}$,
∴$\frac{BP}{BC}$=$\frac{BQ}{BA}$,
∵∠B=∠B,
∴△BPQ∽△BCA,
∴∠BPQ=∠BCA,
∴PQ∥AC.
点评 本题考查四边形综合题、反比例函数的性质、矩形的性质等知识,解题的关键是灵活应用待定系数法确定函数解析式,第三个问题的关键是证明三角形相似,利用相似三角形性质解决问题,属于中考压轴题.

练习册系列答案
相关题目
12.菱形ABCD的一条对角线的长为6,边AB的长是方程x2-7x+12=0的一个根,则菱形ABCD的周长为( )
| A. | 16 | B. | 12 | C. | 12或16 | D. | 无法确定 |
14.汶川地震发生后某市组织了20辆汽车装运食品、药品、生活用品三种救灾物资共100吨到灾民安置点.按计划20辆汽车都要装运,每辆汽车只能装运同一种救灾物资且必须装满.根据下表提供的信息,解答下列问题:
(1)设装运食品的车辆数为x辆,装运药品的车辆数为y辆.求y与x的函数关系式;
(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么,车辆的安排有几种方案?并写出每种安排方案;
(3)在(2)的条件下,若要求总运费最少,应采用哪种安排方案?并求出最少总运费.
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车装载量/吨 | 6 | 5 | 4 |
| 每吨所需运费/元/吨 | 120 | 160 | 100 |
(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么,车辆的安排有几种方案?并写出每种安排方案;
(3)在(2)的条件下,若要求总运费最少,应采用哪种安排方案?并求出最少总运费.
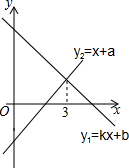 一次函数y1=kx+b与y2=x+a的图象如图,当y1>y2时,x的取值范围是x<3.
一次函数y1=kx+b与y2=x+a的图象如图,当y1>y2时,x的取值范围是x<3. 如图,矩形ABCD中,BC边所在直线上有E、F两点,且BE=CF,请用无刻度的直尺画出该图的对称轴.
如图,矩形ABCD中,BC边所在直线上有E、F两点,且BE=CF,请用无刻度的直尺画出该图的对称轴. 已知:如图,平面直角坐标系中有一个等腰梯形ABCD,且AD∥BC,AB=CD,点A在y轴正半轴上,点B、C在x轴上(点B在点C的左侧),点D在第一象限,AD=3,BC=11,梯形的高为2,双曲线y=$\frac{m}{x}$经过点D,直线y=kx+b经过A、B两点.
已知:如图,平面直角坐标系中有一个等腰梯形ABCD,且AD∥BC,AB=CD,点A在y轴正半轴上,点B、C在x轴上(点B在点C的左侧),点D在第一象限,AD=3,BC=11,梯形的高为2,双曲线y=$\frac{m}{x}$经过点D,直线y=kx+b经过A、B两点.