题目内容
20.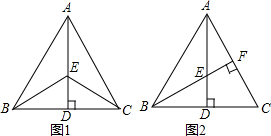 如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,且AE=BC,原题设其它条件不变.求∠BAC的度数.
分析 (1)根据等腰三角形三线合一的性质可得AD垂直平分BC,再根据线段垂直平分线上的点到线段两端点的距离相等可得BE=CE;
(2)根据同角的余角相等求出∠EAF=∠CBF,然后利用“角角边”证明△AEF和△BCF全等,根据全等三角形对应边相等,得到△ABF是等腰直角三角形,根据等腰直角三角形的性质即可得到结论
解答 (1)证明:∵AB=AC,点D是BC的中点,
∴AD垂直平分BC,
∴BE=CE;
(2)证明:∵BF⊥AC,AD⊥BC,
∴∠AFE=∠BFC=∠ADB=90°,
∵∠AEF=∠BED,
∴∠EAF=∠DBE,
在△AEF与△BCF中,$\left\{\begin{array}{l}{∠EAF=∠DBE}\\{∠AFE=∠BFC}\\{AE=BC}\end{array}\right.$,
∴△AEF≌△BCF,
∴AF=BF,
∴△ABF是等腰直角三角形,
∴∠BAC=45°.
点评 本题考查了等腰直角三角形的性质和判定,全等三角形的判定与性质,到线段两端点距离相等的点在线段垂直平分线上的性质,熟记各性质是解题的关键.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
11.不等式组$\left\{\begin{array}{l}x+3>0\\ x-3≤0\end{array}\right.$的解集是( )
| A. | x>-3 | B. | x≤3 | C. | -3<x≤3 | D. | x≥3 |
8.不等式组$\left\{\begin{array}{l}\frac{x-3}{2}≥1\\ 8-x>0\end{array}\right.$的解集是( )
| A. | x≥5 | B. | 5≤x<8 | C. | x>8 | D. | 无解 |
5.为了解某小区居民的用水情况,随机抽查了10户家庭的月用水量,结果如表:
则关于这10户家庭的月用水量,下列说法错误的是( )
| 月用水量(吨) | 4 | 5 | 6 | 9 |
| 户数 | 3 | 4 | 2 | 1 |
| A. | 中位数是5 | B. | 极差是3 | C. | 平均数是5.3 | D. | 众数是5 |
 如图,直线AB和CD相交于点0,则∠AOD=∠BOC.
如图,直线AB和CD相交于点0,则∠AOD=∠BOC. 如图,四边形ABCD是矩形,点E是AD的中点,点F是BC的中点.求证:△ABF≌△CDE.
如图,四边形ABCD是矩形,点E是AD的中点,点F是BC的中点.求证:△ABF≌△CDE.