题目内容
15. 如图,四边形ABCD是矩形,点E是AD的中点,点F是BC的中点.求证:△ABF≌△CDE.
如图,四边形ABCD是矩形,点E是AD的中点,点F是BC的中点.求证:△ABF≌△CDE.
分析 由矩形的性质得出∠B=∠D=90°,AB=CD,AD=BC,由中点的定义得出BF=DE,由SAS证明△ABF≌△CDE即可.
解答 证明:∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB=CD,AD=BC,
∵点E是AD的中点,点F是BC的中点,
∴DE=$\frac{1}{2}$AD BF=$\frac{1}{2}$BC,
∴BF=DE,
在△ABF和△CDE中,
$\left\{\begin{array}{l}AB=CD\\∠B=∠D\\ BF=DE\end{array}\right.$,
∴△ABF≌△CDE(SAS).
点评 本题考查了矩形的性质、全等三角形的判定;熟练掌握矩形的性质,熟记全等三角形的判定方法SAS是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列命题中,是真命题的有( )
①若a>b,则ac>bc;
②$\sqrt{25}$的平方根是±5;
③函数y=x2+$\frac{1}{\sqrt{-x}}$图象上的点P(x,y)一定在第二象限;
④一组数据3,5,4,5,5,6,10的众数和中位数都是5.
①若a>b,则ac>bc;
②$\sqrt{25}$的平方根是±5;
③函数y=x2+$\frac{1}{\sqrt{-x}}$图象上的点P(x,y)一定在第二象限;
④一组数据3,5,4,5,5,6,10的众数和中位数都是5.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.2015年4月某日我市区县的可吸入颗粒物数值统计如下表:
该日这一时刻的可吸入颗粒物数值的众数和中位数分别是( )
| 区县 | 宣威 | 富源 | 沾益 | 马龙 | 师宗 | 罗平 | 陆良 | 会泽 | 麒麟区 | 经开区 |
| 可吸入颗粒物 (mg/m3) | 0.18 | 0.18 | 0.15 | 0.13 | 0.14 | 0.13 | 0.15 | 0.15 | 0.15 | 0.14 |
| A. | 0.15和0.14 | B. | 0.18和0.15 | C. | 0.18和0.14 | D. | 0.15和0.15 |
5. 如图,已知点D是△ABC的重心,连接BD并延长,交AC于点E,若AE=4,则AC的长度为( )
如图,已知点D是△ABC的重心,连接BD并延长,交AC于点E,若AE=4,则AC的长度为( )
 如图,已知点D是△ABC的重心,连接BD并延长,交AC于点E,若AE=4,则AC的长度为( )
如图,已知点D是△ABC的重心,连接BD并延长,交AC于点E,若AE=4,则AC的长度为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
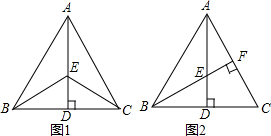 如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.