题目内容
如图，⊙O为△ABC的内切圆，∠C=90°，AO的延长线交BC于点D，AC=4，CD=2，求⊙O的半径．考点：三角形的内切圆与内心
专题：
分析：设圆O与AC的切点为M，圆的半径为r，求得△AOM∽△ADC，利用相似比作为相等关系可列式r：2=（4-r）：4，解之即可．
解答：解：设圆O与AC的切点为M，圆的半径为r，
如图，连接OM，
∵∠C=90°，
∴CM=r，
∵△AOM∽△ADC，
∴OM：CD=AM：AC，
即r：2=（4-r）：4，
解得r=
．
∴⊙O的半径是
．
如图，连接OM，
∵∠C=90°，
∴CM=r，
∵△AOM∽△ADC，
∴OM：CD=AM：AC，
即r：2=（4-r）：4，
解得r=
| 4 |
| 3 |
∴⊙O的半径是
| 4 |
| 3 |
点评：此题考查直角三角形中内切圆的性质及利用相似三角形求内切圆的半径．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
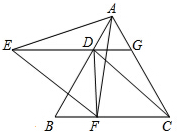如图，△ABC是等边三角形，EG∥BC，DE=DB．EF∥DC，连接DF．
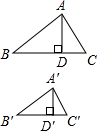如图，△ABC∽△A′B′C′，AD、A′D′分别是它们的高，求证：
已知△ABC的内心为O，∠BOC=110°，则∠BAC=
如图，线段AB=8cm．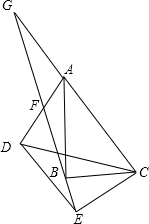
如图，在△ABC和△DEC中，∠ABC=∠DEC=90°，连接AD交射线EB于F，过A作AG∥DE交射线EB于点G，点F恰好是AD中点．
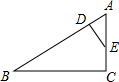如图所示，在△ABC中，点D、E分别是△ABC的边AB、AC上的点，且AD=3，AE=6，DE=5，BD=15，CE=3，BC=15，根据以上条件，你认为∠B=∠AED吗？