题目内容
4.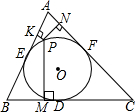 如图,设正△ABC的内切圆⊙O与其三边的切点分别为D、E、F,点P在$\widehat{EF}$上,它到三边AB、BC、CA的距离分别为1、2、x,则x的值为2$\sqrt{2}$+3.
如图,设正△ABC的内切圆⊙O与其三边的切点分别为D、E、F,点P在$\widehat{EF}$上,它到三边AB、BC、CA的距离分别为1、2、x,则x的值为2$\sqrt{2}$+3.
分析 如图,连接AP,EP,FP,AD,分别作PM⊥BC于M,PN⊥AC于N,PK⊥AB于K,于是得到PK=1,PN=2,PM=x,根据等边三角形和切线的性质得到EF是△ABC的中位线,推出△AEF是等边三角形,得到PH⊥EF,设AD交EF于G,则AG=DG=HM,根据三角形的面积得到PM=2PH+3,推出P,H,E,K四点共圆,由圆周角定理得到∠PKH=∠PEH,∠PHK=∠PEK,同理P,H,F,N四点共圆,由圆周角定理得到∠PHN=∠PFN,∠PNH=∠PFH推出△PKH∽△PHN,根据相似三角形的性质得到PH=$\sqrt{PN•PK}$=$\sqrt{2}$即可得到结论.
解答  解:如图,连接AP,EP,FP,AD,分别作PM⊥BC于M,PN⊥AC于N,PK⊥AB于K,
解:如图,连接AP,EP,FP,AD,分别作PM⊥BC于M,PN⊥AC于N,PK⊥AB于K,
则PK=1,PN=2,PM=x,
∵△ABC的内切圆⊙O与其三边的切点分别为D、E、F,
∴EF是△ABC的中位线,
∴△AEF是等边三角形,AD⊥EF,
∴PH⊥EF,
设AD交EF于G,则AG=DG=HM,
∵S△AEF=S△PAE+S△PEF+S△PAF=$\frac{1}{2}$AG•EF,
∴$\frac{1}{2}$AE•PK+$\frac{1}{2}$EF•PH+$\frac{1}{2}$AF•PN=$\frac{1}{2}$AG•EF,
∴(PK+PH+PN)EF=AG•EF,
∴HM=AG=PK=PH+PN=PH+3,
∴PM=2PH+3,
∵PH⊥EF,PN⊥AC,PK⊥AB,
∴P,H,E,K四点共圆,
∴∠PKH=∠PEH,∠PHK=∠PEK,
同理P,H,F,N四点共圆,
∴∠PHN=∠PFN,∠PNH=∠PFH,
∵AE,AF是⊙O的切线,
∴∠PEK=∠PFH,∠PFN=∠PEH,
∴∠PHK=∠PNH,∠PKH=∠PHN,
∴△PKH∽△PHN,
∴$\frac{PH}{PN}=\frac{PK}{PH}$,
即PH=$\sqrt{PN•PK}$=$\sqrt{2}$,
∴PM=2PH+3=2$\sqrt{2}$+3,
即x=2$\sqrt{2}$+3.
故答案为:2$\sqrt{2}$+3.
点评 本题考查了三角形的内切圆与内心,三角形的中位线的性质,等边三角形的性质,勾股定理,四点共圆,圆周角定理,正确的作出辅助线是解题的关键.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案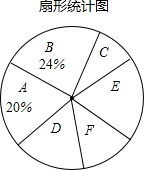 在刚刚闭幕的2016全国“两会”,民生话题依然是社会焦点,某市记者为了了解百姓对“两会民生话题”的聚焦点,随机调查了部分市民,并对调查结果进行整理.绘制了如图所示的统计图表(不完整).
在刚刚闭幕的2016全国“两会”,民生话题依然是社会焦点,某市记者为了了解百姓对“两会民生话题”的聚焦点,随机调查了部分市民,并对调查结果进行整理.绘制了如图所示的统计图表(不完整).頻数分布表
| 组别 | 焦点话题 | 频数(人数) |
| A | 医疗卫生 | 100 |
| B | 食品安全 | m |
| C | 教育住房 | 40 |
| D | 社会保障 | 80 |
| E | 生态环境 | n |
| F | 其他 | 60 |
(1)填空:m=120,n=100.扇形统计图中E组,F组所占的百分比分别为20%、12%
(2)该市现有人口大约800万,请你估计其中关注B组话题的人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注A组话题的概率是多少?
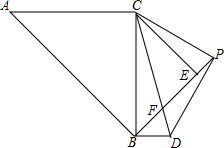 如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=4$\sqrt{2}$,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F
如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=4$\sqrt{2}$,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F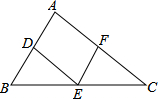 如图,在△ABC中,点D、E、F分别是边AB、BC、CA上的中点,且AB=6cm,AC=8cm,则四边形ADEF的周长等于14cm.
如图,在△ABC中,点D、E、F分别是边AB、BC、CA上的中点,且AB=6cm,AC=8cm,则四边形ADEF的周长等于14cm.