题目内容
 如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB垂直平分线分别交AB,AC及BC的延长线于点D,E,F,求CE和CF的长.
如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB垂直平分线分别交AB,AC及BC的延长线于点D,E,F,求CE和CF的长.考点:线段垂直平分线的性质,勾股定理
专题:
分析:连接BE,可得BE=AE,可设CE=x,在Rt△BCE中由勾股定理可求得CE;在Rt△AFC中可求得CF.
解答: 解:
解:
如图,连接BE,
∴E为线段AD垂直平分线上的点,
∴BE=AE=12,
设CE=x,则BE=AE=12-x,
在Rt△BCE中,由勾股定理可得BC2+CE2=BE2,
即92+x2=(12-x)2,解得x=
,
即CE的长为
;
同理AF=BF,
设FC=y,则AF=BF=9+y,
在Rt△AFC中,由勾股定理可得AC2+FC2=AF2,
即122+y2=(9+y)2,解得y=3.5,
即CF的长为3.5.
 解:
解:如图,连接BE,
∴E为线段AD垂直平分线上的点,
∴BE=AE=12,
设CE=x,则BE=AE=12-x,
在Rt△BCE中,由勾股定理可得BC2+CE2=BE2,
即92+x2=(12-x)2,解得x=
| 21 |
| 8 |
即CE的长为
| 21 |
| 8 |
同理AF=BF,
设FC=y,则AF=BF=9+y,
在Rt△AFC中,由勾股定理可得AC2+FC2=AF2,
即122+y2=(9+y)2,解得y=3.5,
即CF的长为3.5.
点评:本题主要考查线段垂直平分线的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.

练习册系列答案
相关题目
数轴上到原点的距离等于1的点所表示的数是( )
| A、±1 | B、0 | C、1 | D、-1 |
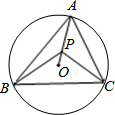 如图,⊙O是△ABC的外接圆,∠BAC=55°,点P在半径AO上(不与A,O重合),则∠BPC可能为
如图,⊙O是△ABC的外接圆,∠BAC=55°,点P在半径AO上(不与A,O重合),则∠BPC可能为 如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,连接EF,EF与AD交于G
如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,连接EF,EF与AD交于G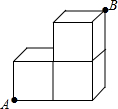 如图是由三个棱长均为1的正方体箱子堆积而成的几何体,在底端的顶点A处有一只蚂蚁,它想吃到顶端的顶点B处的食物,则它沿该几何体表面爬行的最短路程等于( )
如图是由三个棱长均为1的正方体箱子堆积而成的几何体,在底端的顶点A处有一只蚂蚁,它想吃到顶端的顶点B处的食物,则它沿该几何体表面爬行的最短路程等于( )