题目内容
1.将一个半径为10cm的圆分成3个扇形,其圆心角的比1:2:3.求:(1)各个扇形的圆心角的度数;
(2)其中最小一个扇形的面积(结果保留π).
分析 (1)三个圆心角的度数之和为360°,据此进行解答;
(2)圆心角最小的扇形的面积最小,根据扇形的面积公式进行解答.
解答 解:(1)设三个圆心角的度数分别是x、2x、3x,则
x+2x+3x=360°,
解得x=60°.
故这三个扇形的圆心角分别是:60°、120°、180°;
(2)圆心角为60°的扇形的面积最小,其面积为:$\frac{60•π×1{0}^{2}}{360}$=$\frac{50}{3}$π(cm2).
点评 本题考查了扇形的面积的计算,认识平面图形,掌握周角的定义和扇形的面积即可解答该题,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
9.根据下列表述,能确定具体位置的是( )
| A. | 奥斯卡影院2号厅3排 | B. | 汝南县汝宁大街 | ||
| C. | 东经118° | D. | 天中山北偏东60°,10km处 |
16.在下列实数中,无理数是( )
| A. | 0 | B. | -$\frac{22}{7}$ | C. | $\sqrt{2}$ | D. | $\sqrt{9}$ |
10.在平面直角坐标系中,点P的坐标为(3,-1),那么点P在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
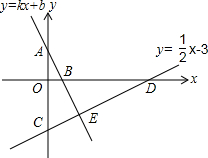 如图,点A、B的坐标分别为(0,2),(1,0),直线y=$\frac{1}{2}x$-3与坐标轴交于C、D两点.
如图,点A、B的坐标分别为(0,2),(1,0),直线y=$\frac{1}{2}x$-3与坐标轴交于C、D两点.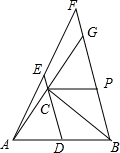 如图,△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=$\frac{1}{3}$CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
如图,△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=$\frac{1}{3}$CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.