题目内容
2.若|x+3|+|y-2|+|2z+1|=0,求(xy-yz)(y-x+z)的值.分析 根据非负数的和为零,可得每个非负数同时为零,可得x、y、z的值,根据代数式求值,可得答案.
解答 解:由题意,得
x+3=0,y-2=0,2z+1=0.
解得x=-3,y=2,z=-$\frac{1}{2}$.
(xy-yz)(y-x+z)=[-3×2-2×(-$\frac{1}{2}$)][2-(-3)+(-$\frac{1}{2}$)]
=-5×$\frac{9}{2}$
=-$\frac{45}{2}$.
点评 本题考查了非负数党的性质,利用非负数的和为零得出每个非负数同时为零是解题关键.

练习册系列答案
相关题目
 如图,点B、E、C、F在同一直线上,AB=DE,∠ABC=∠DEF,BE=CF,求证:AC∥DF.
如图,点B、E、C、F在同一直线上,AB=DE,∠ABC=∠DEF,BE=CF,求证:AC∥DF.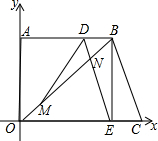 如图,在直角梯形OABC中,已知B、C两点的坐标分别为B(8,6)、C(10,0),动点M由原点O出发沿OB方向匀速运动,速度为1单位/秒;同时,线段DE由BC出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM,设运动时间为t秒(0<t<8)
如图,在直角梯形OABC中,已知B、C两点的坐标分别为B(8,6)、C(10,0),动点M由原点O出发沿OB方向匀速运动,速度为1单位/秒;同时,线段DE由BC出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM,设运动时间为t秒(0<t<8)