题目内容
13.已知多边形的内角和等于1440°,求:(1)这个多边形的边数;
(2)过一个顶点有几条对角线;
(3)总对角线条数.
分析 (1)利用多边形的内角和定理即可列方程求解;
(2)根据多边形的对角线的定义,不相邻的两个顶点之间的连线就是对角线即可求解;
(3)根据(2)的结果即可直接求得.
解答 解:(1)设边数是n,根据题意得(n-2)180=1440,
解得:n=10.
则这个多边形是十边形;
(2)过一个顶点的对角线的条数是10-3=7;
(3)对角线的总条数是:$\frac{1}{2}$×10×7=35(条).
点评 本题考查了多边形的内角和定理以及对角线的条数的计算,理解定理,求得多边形的边数是关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
3.体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
(1)全班有多少同学?
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几?
(4)画出适当的统计图表示上面的信息.
| 次数 | 60≤x<90 | 90≤x<120 | 120≤x<150 | 150≤x<180 | 180≤x<210 |
| 频数 | 16 | 25 | 9 | 7 | 3 |
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几?
(4)画出适当的统计图表示上面的信息.
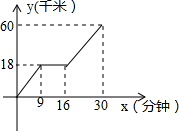 如图,是某汽车行驶的路程y(千米)与时间x(分钟)的函数关系图象,观察图中所提供的信息,解答下列问题.
如图,是某汽车行驶的路程y(千米)与时间x(分钟)的函数关系图象,观察图中所提供的信息,解答下列问题.