题目内容
12. 如图,点B、E、C、F在同一直线上,AB=DE,∠ABC=∠DEF,BE=CF,求证:AC∥DF.
如图,点B、E、C、F在同一直线上,AB=DE,∠ABC=∠DEF,BE=CF,求证:AC∥DF.
分析 求出BC=EF,然后利用“边角边”证明△ABC和△DEF全等,根据全等三角形对应角相等可得∠ACB=∠F,再根据同位角相等,两直线平行证明即可.
解答 证明:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中,$\left\{\begin{array}{l}{AB=DE}\\{∠ABC=∠DEF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴∠ACB=∠F,
∴AC∥DF.
点评 本题考查了全等三角形的判定与性质,平行线的判定,熟练掌握三角形全等的判定方法是解题的关键.

练习册系列答案
相关题目
7.已知|a|=4,|b|=3,|a+b|=-(a+b),则a-b=( )
| A. | -7 | B. | -1 | C. | -7或-1 | D. | ±7或±1 |
 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).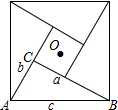 在Rt△ABC中,∠ACB=90°,BC=a,AC=b.AB=c,将Rt△ABC绕点O依次旋转90°、180°和270°,构成的图形如图所示,该图是我国古代数学家赵爽制作的“勾股圆方图”,也被称作“赵爽弦图”,它是我国最早对勾股定理证明的记载,也成为了2002年在北京召开的国际数学家大会的会标设计的主要依据.
在Rt△ABC中,∠ACB=90°,BC=a,AC=b.AB=c,将Rt△ABC绕点O依次旋转90°、180°和270°,构成的图形如图所示,该图是我国古代数学家赵爽制作的“勾股圆方图”,也被称作“赵爽弦图”,它是我国最早对勾股定理证明的记载,也成为了2002年在北京召开的国际数学家大会的会标设计的主要依据.