题目内容
4．已知函数y=ax2与函数y=-$\frac{2}{3}$x2+c的形状完全相同，且抛物线y=ax2沿对称轴平移2个单位就能与y=-$\frac{2}{3}$x2+c完全重合，求这两个函数的解析式．分析 由函数y=ax2与函敷y=-$\frac{2}{3}$x2+c的形状完全相同，可知a=-$\frac{2}{3}$，从而求得函数y=ax2与的解析式为y=-$\frac{2}{3}$x2；由抛物线y=-$\frac{2}{3}$x2的对称轴为y轴，根据上加下减的平移规律即可求得函数y=-$\frac{2}{3}$x2+c的解析式．
解答 解：∵函数y=ax2与函敷y=-$\frac{2}{3}$x2+c的形状完全相同，
∴a=-$\frac{2}{3}$，
∴函数为y=-$\frac{2}{3}$x2；
又∵抛物线y=-$\frac{2}{3}$x2的对称轴为y轴，
∴抛物线y=-$\frac{2}{3}$x2的图象沿对称轴平移两个单位后就能与y=-$\frac{2}{3}$x2+c的图象完全重合，
∴平移后的二次函数的表达式为y=-$\frac{2}{3}$x2±2．
∴这两个函数的解析式为y=-$\frac{2}{3}$x2和y=-$\frac{2}{3}$x2±2．
点评 本题考查的是二次函数的图象与几何变换，熟知图形平移不变性的性质是解答此题的关键．
练习册系列答案
相关题目
有这样一个小游戏，如图1-4号四个气球上分别贴有四个结论：①已知a=-5，|a|=|b|，则b的值等于-5；②如果m=-2015，那么-m的值是2015；③一个数的绝对值越大，这个数就越大；④$\frac{1}{5}$的相反数是-0.2，将贴有正确结论的气球全部打爆者获胜，你认为应该打爆的气球是②④（写出气球的号数）．
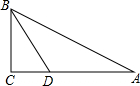如图．已知△ABC中，∠C=90°，∠A=30°，BD平分∠CBA，且交AC于点D，AC=1．求AD的长．