题目内容
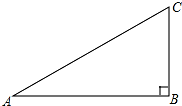 如图,在直角三角形ABC中,∠ABC=90°
如图,在直角三角形ABC中,∠ABC=90°(1)先作∠ACB的平分线;设它交AB边于点O,再以点O为圆心,OB为半径作⊙O.
(2)证明:AC是所作⊙O的切线.
考点:切线的判定,作图—复杂作图
专题:证明题
分析:(1)先作角平分线OB交AB于D,再作⊙O,如图;
(2)作OD⊥AC于D,根据角平分线的性质得OD=OB,利用OB为圆的半径和切线的判定定理即可得到AC是所作⊙O的切线.
(2)作OD⊥AC于D,根据角平分线的性质得OD=OB,利用OB为圆的半径和切线的判定定理即可得到AC是所作⊙O的切线.
解答:(1)解:如图;

(2)证明:作OD⊥AC于D,如图,
∵CO是∠ACB的平分线
∴OD=OB,
而OB为⊙O的半径,
∴AC为⊙O的切线.

(2)证明:作OD⊥AC于D,如图,
∵CO是∠ACB的平分线
∴OD=OB,
而OB为⊙O的半径,
∴AC为⊙O的切线.
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线;在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.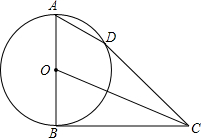 如图,已知AB是⊙O的直径,点D在⊙O上,C是⊙O外一点.若AD∥OC,直线BC与⊙O相交,判断直线CD与⊙O的位置关系,并说明理由.
如图,已知AB是⊙O的直径,点D在⊙O上,C是⊙O外一点.若AD∥OC,直线BC与⊙O相交,判断直线CD与⊙O的位置关系,并说明理由.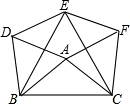 如图,以△ABC的三边为边,在BC边的同侧作等边△DBA,△EBC,△FAC.
如图,以△ABC的三边为边,在BC边的同侧作等边△DBA,△EBC,△FAC.