��Ŀ����
10��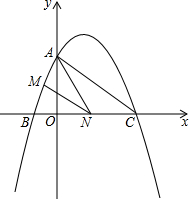 ��ͼ����֪���κ���y=ax2+$\frac{3}{2}$x+c��ͼ����y�ύ�ڵ�A��0��4������x�ύ�ڵ�B��C����C������Ϊ��8��0��������AC��AC��
��ͼ����֪���κ���y=ax2+$\frac{3}{2}$x+c��ͼ����y�ύ�ڵ�A��0��4������x�ύ�ڵ�B��C����C������Ϊ��8��0��������AC��AC����1����ֱ��д�����κ���y=ax2+$\frac{3}{2}$x+c�ı���ʽ��
��2���жϡ�ABC����״����˵�����ɣ�
��3������N���߶�BC���˶��������B��C�غϣ�������N��NM��AC����AB�ڵ�M������AMN������ʱ�����ʱN�����꣮
���� ��1������A�͵�C�����������������ߵĽ���ʽ�����a��c��ֵ���ɣ�
��2������õ�B�����꣬�Ӷ��õ�BC=10��Ȼ�����ݹ��ɶ��������AB2��AC2��ֵ��������ݹ��ɶ������涨�������жϼ��ɣ�
��3�����N������Ϊ��n��0����-2��n��8������BN=n+2��CN=8-n������ƽ���߷��߶γɱ��������ɵõ�$\frac{AM}{AB}$=$\frac{NC}{BC}$=$\frac{8-n}{10}$��Ȼ�����ݵȸߵ����������ε�����ȵ��ڵױߵij��ȱȿɵõ�S��AMN��n�ĺ�����ϵʽ��������ö��κ��������ʿ���á�AMN�����ȡ�����ֵʱ��N�����꣮
��� �⣺��1������A�͵�C���������ã�$\left\{\begin{array}{l}{c=4}\\{64a+12+c=0}\end{array}\right.$��
��ã�a=-$\frac{1}{4}$��c=4��
��ö��κ����Ľ���ʽΪy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
��2����y=0�ã�-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=0����ã�x=-2��x=8��
���B��-2��0����
��BC=10��
��Rt��AOB��Rt��AOC�У����ݹ��ɶ�����֪��AB2=OB2+AO2=20��AC2=OA2+OC2=80��
��AB2+AC2=BC2��
���ABCΪֱ�������Σ�
��3�����N��������n��0����-2��n��8������BN=n+2��CN=8-n��
��MN��AC��
��$\frac{AM}{AB}$=$\frac{NC}{BC}$=$\frac{8-n}{10}$��
��AO=4��BC=10��
��S��ABC=$\frac{1}{2}$BC•AO=$\frac{1}{2}$��4��10=20��
��S��ABN=$\frac{n+2}{10}$S��ABC=2��n+2����
��S��AMN=$\frac{8-n}{10}$S��AMN=$\frac{1}{5}$��8-n����n+2��=-$\frac{1}{5}$��n-3��2+5��
�൱n=3ʱ����N��3��0��ʱ����AMN�����������ֵΪ5��
���� ������Ҫ������Ƕ��κ����������ۺ�Ӧ�ã��������ҪӦ���˹��ɶ��������ɶ������涨����ƽ���߷��߶γɱ����������г���AMN��������N�ĺ�����n֮��Ĺ�ϵʽ�ǽ���Ĺؼ���

 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д�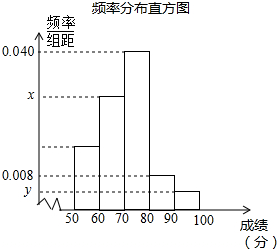 Ϊ�μ�ѧУ�ġ��Ұ���ʫ�ʡ�֪ʶ������С�����ڰ༶��֯��һ�ι�ʫ��֪ʶ���ԣ�����ȫ��ͬѧ�ķ������÷�ȡ������������Ϊ100�֣�����ͳ�ƣ������Ǹ�����β��Գɼ������IJ�������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ��
Ϊ�μ�ѧУ�ġ��Ұ���ʫ�ʡ�֪ʶ������С�����ڰ༶��֯��һ�ι�ʫ��֪ʶ���ԣ�����ȫ��ͬѧ�ķ������÷�ȡ������������Ϊ100�֣�����ͳ�ƣ������Ǹ�����β��Գɼ������IJ�������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ�� | ��� | ���� | Ƶ�� | Ƶ�� |
| 1 | ��50��x��60 | 9 | 0.18 |
| 2 | ��60��x��70 | a | |
| 3 | ��70��x��80 | 20 | 0.40 |
| 4 | ��80��x��90 | 0.08 | |
| 5 | ��90��x��100 | 2 | b |
| �ϼ� |
��1�����a��b��x��y��ֵ��
��2����Ҫ��С����С������λ�ɼ������ͬѧ�����ѡȡ��λ�μӾ��������á��б���������״ͼ�����С����С��ͬʱ��ѡ�еĸ��ʣ���ע����λͬѧ����A��B��C��D��E��ʾ������С��ΪA��С��ΪB��
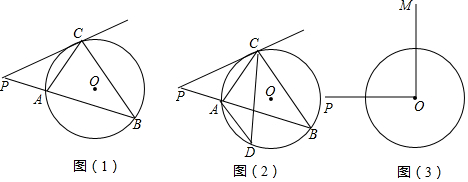
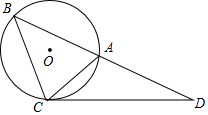 ��ͼ��ʾ����ABC�����Բ��O�İ뾶Ϊ2������C����ACD=��ABC����BA���ӳ����ڵ�D������ABC=45�㣬��D=30�㣮
��ͼ��ʾ����ABC�����Բ��O�İ뾶Ϊ2������C����ACD=��ABC����BA���ӳ����ڵ�D������ABC=45�㣬��D=30�㣮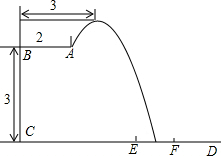 2016����Լ���˻ᣬ�й���ˮ��Ӯ��8����Ŀ�е�7����ƣ�����ɼ���ȡ���벻��������ѵ����ij��ˮ�˶�Ա�ڽ�����ˮѵ��ʱ�����壨����һ�㣩�ڿ��е��˶�·������ͼ��ʾ��һ�������ߣ���֪����AB��Ϊ2�ף������ˮ��CD�ĸ�BCΪ3�ף�ѵ��ʱ��ˮ��������������ˮƽ����1��ʱ�ﵽ��ˮ�����߶�k�ף�����CDΪ���ᣬCBΪ���Ὠ��ֱ������ϵ��
2016����Լ���˻ᣬ�й���ˮ��Ӯ��8����Ŀ�е�7����ƣ�����ɼ���ȡ���벻��������ѵ����ij��ˮ�˶�Ա�ڽ�����ˮѵ��ʱ�����壨����һ�㣩�ڿ��е��˶�·������ͼ��ʾ��һ�������ߣ���֪����AB��Ϊ2�ף������ˮ��CD�ĸ�BCΪ3�ף�ѵ��ʱ��ˮ��������������ˮƽ����1��ʱ�ﵽ��ˮ�����߶�k�ף�����CDΪ���ᣬCBΪ���Ὠ��ֱ������ϵ��