题目内容
19. 已知矩形OABC在平面直角坐标系中的位置如图所示,AB=3,BC=2,点D在边AB上运动,把矩形沿线段CD折叠,点B的对应点为B′,则使△B′OC成为等腰三角形的点B′的坐标为(-$\frac{3}{2}$,$\frac{\sqrt{7}}{2}$).
已知矩形OABC在平面直角坐标系中的位置如图所示,AB=3,BC=2,点D在边AB上运动,把矩形沿线段CD折叠,点B的对应点为B′,则使△B′OC成为等腰三角形的点B′的坐标为(-$\frac{3}{2}$,$\frac{\sqrt{7}}{2}$).
分析 作B′E⊥OC于E,根据等腰三角形的性质得到OE=$\frac{1}{2}$OC,根据翻转变换的性质求出B′O=2,根据勾股定理求出B′E,得到答案.
解答 解: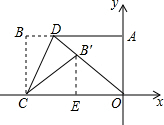 作B′E⊥OC于E,
作B′E⊥OC于E,
∵△B′OC为等腰三角形,
∴OE=$\frac{1}{2}$OC=$\frac{3}{2}$,
由翻转变换的性质可知,B′C=BC=2,
∴B′O=2,
由勾股定理得,B′E=$\sqrt{B′{O}^{2}-O{E}^{2}}$=$\frac{\sqrt{7}}{2}$,
∴点B′的坐标为:(-$\frac{3}{2}$,$\frac{\sqrt{7}}{2}$),
故答案为:(-$\frac{3}{2}$,$\frac{\sqrt{7}}{2}$).
点评 本题考查的是翻转变换的性质、等腰三角形的性质,掌握翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
8.用棋子摆出下列一组图形:
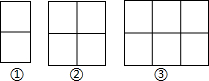
(1)填写下表:
(2)照这样的方式摆下去,写出摆第n个图形棋子的枚数;
(3)如果某一图形共有102枚棋子,你知道它是第几个图形吗?

(1)填写下表:
| 图形编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 图形中的棋子 | 6 | 9 | 12 | 15 | 18 | 21 |
(3)如果某一图形共有102枚棋子,你知道它是第几个图形吗?
 已知:如图,在平面直角坐标系xOy中,△OBC是等腰三角形,底边OC落在x轴上,点C坐标为(2,0).直线AB与反比例函数都经过第一象限的点B,且A(-1,0),直线AB交y轴于点D,若S△BOC=4.
已知:如图,在平面直角坐标系xOy中,△OBC是等腰三角形,底边OC落在x轴上,点C坐标为(2,0).直线AB与反比例函数都经过第一象限的点B,且A(-1,0),直线AB交y轴于点D,若S△BOC=4.