题目内容
11. 已知二次函数y=ax2+bx+c (a≠0)的图象如图所示,有下列5个结论:
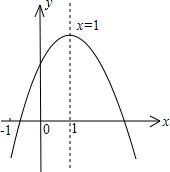
已知二次函数y=ax2+bx+c (a≠0)的图象如图所示,有下列5个结论:①abc<0; ②b<a+c; ③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数),其中结论正确的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①图象开口向下,与y轴交于正半轴,对称轴为x=1,能得到:a<0,c>0,-$\frac{b}{2a}$=1,
∴b=-2a>0,
∴abc<0,此结论正确;
②当x=-1时,由图象知y<0,
把x=-1代入解析式得:a-b+c<0,
∴b>a+c,
∴②错误;
③图象开口向下,与y轴交于正半轴,对称轴为x=1,
能得到:a<0,c>0,-$\frac{b}{2a}$=1,
所以b=-2a,
所以4a+2b+c=4a-4a+c>0.
∴③正确;
④∵由①②知b=-2a且b>a+c,
∴2c<3b,④正确;
⑤∵x=1时,y=a+b+c(最大值),
x=m时,y=am2+bm+c,
∵m≠1的实数,
∴a+b+c>am2+bm+c,
∴a+b>m(am+b).
∴⑤错误.
故选:B.
点评 此题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
19.对于任意实数x,点P(x,x2+4x+3)一定不在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.嘉淇同学大学毕业后借助低息贷款创业,他向银行贷款30000元,分12个月还清贷款,月利率是0.2%,银行规定的还款方式为“等额本金法”,即每月除归还等额的本金为30000÷12=2500元外,还需要归还本月还款前的本金的利息,下面是还款的部分明细.
第1个月,由于本月还款前的本金是30000元,则本月应归还的利息为30000×0.2%=60元,本月应归还的本息和为2500+60=2560元;
第2个月,由于本月还款前的本金是27500元,则本月应归还的利息为27500×0.2%=55元,本月应归还的本息和为2500+55=2555元.
…
根据上述信息,则
(1)在空格处直接填写结果:
(2)设第x个月应归还的利息是y元,求y关于x的函数关系式,并写出x的取值范围;
(3)嘉淇将创业获利的2515元用于还款,则恰好可以用于还清第几个月的本息和?
第1个月,由于本月还款前的本金是30000元,则本月应归还的利息为30000×0.2%=60元,本月应归还的本息和为2500+60=2560元;
第2个月,由于本月还款前的本金是27500元,则本月应归还的利息为27500×0.2%=55元,本月应归还的本息和为2500+55=2555元.
…
根据上述信息,则
(1)在空格处直接填写结果:
| 月数 | 第1个月 | 第2个月 | … | 第5个月 | … |
| 还款前的本金(单位:元) | 30000 | 27500 | … | 20000 | … |
| 应归还的利息(单位:元) | 60 | 55 | … | 40 | … |
(3)嘉淇将创业获利的2515元用于还款,则恰好可以用于还清第几个月的本息和?
19.能构成三角形的是( )
| A. | 2、3、4 | B. | 5、3、8 | C. | 1、3、5 | D. | 1、2、3 |
 已知:如图,AC⊥BC,DE⊥BC,求证:∠BDE=∠A.
已知:如图,AC⊥BC,DE⊥BC,求证:∠BDE=∠A.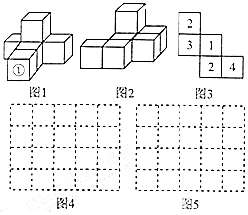 按要求完成下列问题:
按要求完成下列问题: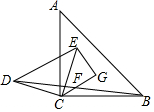 如图,△ABC和△DEC都是等腰直角三角形,连接BD,F是BD的中点,连接CF并延长至G,使FG=CF,连接EC,CE=10,CF=4,EG=6,则S△ABC=2$\sqrt{130}$.
如图,△ABC和△DEC都是等腰直角三角形,连接BD,F是BD的中点,连接CF并延长至G,使FG=CF,连接EC,CE=10,CF=4,EG=6,则S△ABC=2$\sqrt{130}$.