题目内容
1.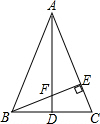 如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE.
如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE.
分析 根据等腰三角形的性质,由AB=AC,D是BC中点得到AD⊥BC,易得∠ADC=∠BEC=90°,再证明∠FAE=∠CBE,于是根据有两组角对应相等的两个三角形相似即可得到结论.
解答 证明:∵AB=AC,D是BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∴∠FAE+∠AFE=90°,
∵BE⊥AC,
∴∠BEC=90°,
∴∠CBE+∠BFD=90°,
∵∠AFE=∠BFD,
∴∠FAE=∠CBE,
∴△AFE∽△BCE.
点评 本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了等腰三角形的性质,证题的关键是挖掘题目的隐藏条件:对顶角相等.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13.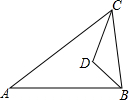 如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D=3∠A,则∠A=( )
如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D=3∠A,则∠A=( )
 如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D=3∠A,则∠A=( )
如图,在△ABC中,BD平分∠ABC,CD平分∠BCA,若∠D=3∠A,则∠A=( )| A. | 32° | B. | 36° | C. | 40° | D. | 44° |
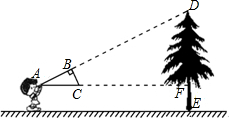 如图,小夏同学用自己做的直角三角形纸板ABC测量树的高度DE,小夏不断调整自己的位置,最终使纸板ABC的斜边AC保持水平,并且边AB与点D在同一直线上,已知纸板的两条直角边AB=0.4m,BC=0.2m,测得边AF=8m,AC离地面的高度为1.5m.求树高.
如图,小夏同学用自己做的直角三角形纸板ABC测量树的高度DE,小夏不断调整自己的位置,最终使纸板ABC的斜边AC保持水平,并且边AB与点D在同一直线上,已知纸板的两条直角边AB=0.4m,BC=0.2m,测得边AF=8m,AC离地面的高度为1.5m.求树高. 如图,△ABC中,∠A=90°,AB=AC,BC=45,长方形DEFG为△ABC的内接长方形,且DG:DE=5:2.求DE、EF的长.
如图,△ABC中,∠A=90°,AB=AC,BC=45,长方形DEFG为△ABC的内接长方形,且DG:DE=5:2.求DE、EF的长.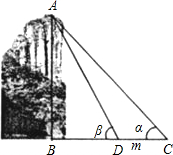 如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).当α=44°,β=61°,m=50米时,求h的值.(精确到1米)
如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).当α=44°,β=61°,m=50米时,求h的值.(精确到1米)