题目内容
12.有三种长度分别为三个连续整数的木棒,小明利用中等长度的木棒摆成了一个正方形,小刚用其余两种长度的木棒摆出了一个长方形,则他们两人谁摆的面积大?( )| A. | 小刚 | B. | 小明 | C. | 同样大 | D. | 无法比较 |
分析 可设三个木棒的长度分别为x-1、x、x+1,分别表示出两个图形的面积,再用作差法进行比较大小即可.
解答 解:设三个木棒的长度分别为x-1、x和x+1,
则小明所摆正方形的面积为x2,小刚所摆长方形的面积为(x+1)(x-1),
∵x2-(x+1)(x-1)=x2-(x2-1)=x2-x2+1=1>0,
∴x2>(x+1)(x-1),
∴小明所摆的正方形的面积大于小刚所摆长方形的面积,
故选B.
点评 本题主要考查平方差公式的应用,掌握平方差公式是解题的关键,注意作差法比较大小的应用.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
2.一个两位数,十位上的数字x比个位上的数字y大1,若颠倒个位与十位数字的位置,得到新数比原数小9,求这个两位数列出的方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x-y=1}\\{(x+y)+(y+x)=9}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=y+1}\\{10x+y=y+x+9}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=1}\\{10x+y=10y+x+9}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=y+1}\\{10x+y=10y+x+9}\end{array}\right.$ |
 一瓶装满的可乐,喝了一些后,把瓶盖拧紧后倒置放平,如图,喝了这瓶可乐的44%.(百分号前保留整数)
一瓶装满的可乐,喝了一些后,把瓶盖拧紧后倒置放平,如图,喝了这瓶可乐的44%.(百分号前保留整数)
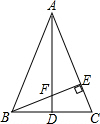 如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE.
如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE.