题目内容
11.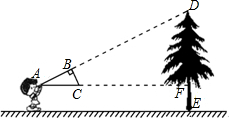 如图,小夏同学用自己做的直角三角形纸板ABC测量树的高度DE,小夏不断调整自己的位置,最终使纸板ABC的斜边AC保持水平,并且边AB与点D在同一直线上,已知纸板的两条直角边AB=0.4m,BC=0.2m,测得边AF=8m,AC离地面的高度为1.5m.求树高.
如图,小夏同学用自己做的直角三角形纸板ABC测量树的高度DE,小夏不断调整自己的位置,最终使纸板ABC的斜边AC保持水平,并且边AB与点D在同一直线上,已知纸板的两条直角边AB=0.4m,BC=0.2m,测得边AF=8m,AC离地面的高度为1.5m.求树高.
分析 证明△ABC∽△AFD,然后利用相似比计算出DF,再计算DF+EF即可.
解答 解:∵∠BAC=∠FAD,
∴△ABC∽△AFD,
∴$\frac{AB}{AF}$=$\frac{BC}{DF}$,即$\frac{0.4}{8}$=$\frac{0.2}{DF}$,
∴DF=4,
∴DE=DF+EF=4+1.5=5.5(m).
答:树高为5.5m.
点评 本题考查了相似三角形的应用:借助标杆或直尺测量物体的高度.利用杆或直尺测量物体的高度就是利用杆或直尺的高(长)作为三角形的边,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.在下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
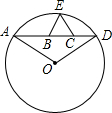 如图,A、D、E是⊙O上的三个点,且∠AOD=120°,B、C是弦AD上两点,BC=$\sqrt{3}$,△BCE是等边三角形.若设AB=x,CD=y,则y与x的函数关系式是y=$\frac{3}{x}$.
如图,A、D、E是⊙O上的三个点,且∠AOD=120°,B、C是弦AD上两点,BC=$\sqrt{3}$,△BCE是等边三角形.若设AB=x,CD=y,则y与x的函数关系式是y=$\frac{3}{x}$. 一瓶装满的可乐,喝了一些后,把瓶盖拧紧后倒置放平,如图,喝了这瓶可乐的44%.(百分号前保留整数)
一瓶装满的可乐,喝了一些后,把瓶盖拧紧后倒置放平,如图,喝了这瓶可乐的44%.(百分号前保留整数)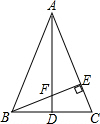 如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE.
如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE.