题目内容
6. 如图,△ABC中,∠A=90°,AB=AC,BC=45,长方形DEFG为△ABC的内接长方形,且DG:DE=5:2.求DE、EF的长.
如图,△ABC中,∠A=90°,AB=AC,BC=45,长方形DEFG为△ABC的内接长方形,且DG:DE=5:2.求DE、EF的长.
分析 过点A作AH⊥BC交DG于点P,垂足为H,首先利用等腰三角形的性质可知点H是BC的中点,从而可求得AH=$\frac{45}{2}$,由DG∥BC,可知△ADG∽△ABC,然后利用相似三角形的性质列出比例式,解得求得DE和DG的长度.
解答 解:过点A作AH⊥BC交DG于点P,垂足为H.
∵AB=AC,AH⊥BC,
∴BH=CH.
又∵∠A=90°,
∴AH=$\frac{1}{2}BC=\frac{1}{2}×45=\frac{45}{2}$.
∵DG∥BC,
∴△ADG∽△ABC.
∴$\frac{DG}{BC}=\frac{AP}{AH}$.
设DG=5x,DE=2x,则$\frac{5x}{45}=\frac{\frac{45}{2}-2x}{\frac{45}{2}}$,解得:x=5.
∴DE=10,EF=25.
点评 本题主要考查的是相似三角形的性质,利用相似三角形的性质列出比例式,从而解得x的值是解题的关键.

练习册系列答案
相关题目
11. 如图,若AB=AC,∠1=∠2,则下列条件不能使△ABD≌△ACE的是( )
如图,若AB=AC,∠1=∠2,则下列条件不能使△ABD≌△ACE的是( )
 如图,若AB=AC,∠1=∠2,则下列条件不能使△ABD≌△ACE的是( )
如图,若AB=AC,∠1=∠2,则下列条件不能使△ABD≌△ACE的是( )| A. | AE=AD | B. | ∠B=∠C | C. | ∠E=∠D | D. | BD=CE |
16.一个三位数a写在两位数b的右边构成一个五位数,则这个五位数可表示为( )
| A. | 10b+a | B. | 100b+a | C. | 1000b+a | D. | 100b+10a |
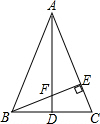 如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE.
如图,△ABC中,AB=AC,BE⊥AC于E,D是BC中点,连接AD与BE交于点F,求证:△AFE∽△BCE.