题目内容
20．因式分解：-9（m+n）3+12（m+n）2-4（m+n）=-（m+n）（3m+3n-2）2．分析 原式提取公因式，再利用完全平方公式分解即可．
解答 解：原式=-（m+n）[9（m+n）2-12（m+n）+4]=-（m+n）（3m+3n-2）2．
故答案为：-（m+n）（3m+3n-2）2
点评 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
10．下列说法不一定成立的是（ ）
| A． | 若a＞b，则a+c＞b+c | B． | 若a+c＞b+c，则a＞b | C． | 若a＞b，则a2c＞bc2 | D． | 若a2c＞bc2，则a＞b |
15．在下列各数中，使不等式x-1＞2成立的数为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{5}$ | D． | $\sqrt{11}$ |
5．
阅读下列材料：
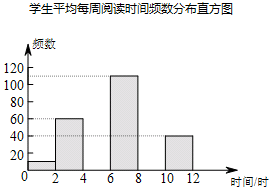
为引导学生广泛阅读古今文学名著，某校开展了读书月活动．学生会随机调查了部分学生平均每周阅读时间的情况，整理并绘制了如图的统计图表：
学生平均每周阅读时间频数分布表
请根据以上信息，解答下列问题：
（1）在频数分布表中，a=80，b=0.275；
（2）补全频数分布直方图；
（3）如果该校有1 600名学生，请你估计该校平均每周阅读时间不少于6小时的学生大约有1000人．
阅读下列材料：为引导学生广泛阅读古今文学名著，某校开展了读书月活动．学生会随机调查了部分学生平均每周阅读时间的情况，整理并绘制了如图的统计图表：
学生平均每周阅读时间频数分布表
| 平均每周阅读时间x（时） | 频数 | 频率 |
| 0≤x＜2 | 10 | 0.025 |
| 2≤x＜4 | 60 | 0.150 |
| 4≤x＜6 | a | 0.200 |
| 6≤x＜8 | 110 | b |
| 8≤x＜10 | 100 | 0.250 |
| 10≤x＜12 | 40 | 0.100 |
| 合计 | 400 | 1.000 |
（1）在频数分布表中，a=80，b=0.275；
（2）补全频数分布直方图；
（3）如果该校有1 600名学生，请你估计该校平均每周阅读时间不少于6小时的学生大约有1000人．
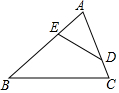如图，在△ABC中，D，E分别是AC和AB上的点，AD=3cm，AC=4cm，AE=2cm，且$\frac{AD}{AB}$=$\frac{AE}{AC}$，则AB=6cm，BE=4cm．
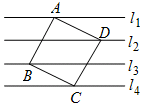如图，已知直线l1∥l2∥l3∥l4，且相邻两条平行直线间的距离都是d，如果正方形ABCD的四个顶点分别在四条直线上，且面积都是1，则d=$\frac{\sqrt{5}}{5}$．
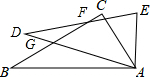如图，△ABC≌△ADE，∠DAC=60°，∠BAE=100°，BC分别交AD、DE于点G、F，求∠DFB的度数．