题目内容
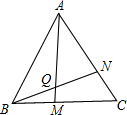如图，△ABC为等边三角形，点M，N分别在BC，AC上，且BM=CN，AM与BN交于Q点．则∠AQN的度数为考点：全等三角形的判定与性质,等边三角形的性质
专题：
分析：如图，证明△ABM≌△BCN，结合三角形外角的性质即可解决问题．
解答：解：∵△ABC为等边三角形，
∴AB=BC，∠ABM=∠BCN=60°，
在△ABM与△BCN中，
，
∴△ABM≌△BCN（SAS），
∴∠BAQ=∠MBQ，
∴∠AQN=∠ABQ+∠BAQ
=∠ABQ+∠MBQ=60°，
即∠AQN的度数为60°，
故答案为：60°．
解：∵△ABC为等边三角形，∴AB=BC，∠ABM=∠BCN=60°，
在△ABM与△BCN中，
|
∴△ABM≌△BCN（SAS），
∴∠BAQ=∠MBQ，
∴∠AQN=∠ABQ+∠BAQ
=∠ABQ+∠MBQ=60°，
即∠AQN的度数为60°，
故答案为：60°．
点评：该命题以等边三角形为载体，以等边三角形的性质、全等三角形的判定及其应用为考查的核心构造而成；解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
