题目内容
3.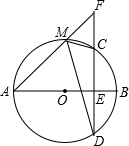 已知:如图,AB是⊙O的直径,CD为弦,且AB⊥CD于E,F为DC延长线上一点,连结AF交⊙O于M.
已知:如图,AB是⊙O的直径,CD为弦,且AB⊥CD于E,F为DC延长线上一点,连结AF交⊙O于M.求证:∠AMD=∠FMC.
分析 首先连接BM,由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠AMB=∠BMF=90°,又由AB⊥CD于E,可得:$\widehat{BC}$=$\widehat{BD}$,继而证得∠CMB=∠BMD,则可证得结论.
解答 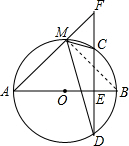 证明:连结BM,
证明:连结BM,
∵AB是⊙O的直径,
∴∠AMB=∠BMF=90°,
又∵AB⊥CD于E,
∴$\widehat{BC}$=$\widehat{BD}$,
∴∠CMB=∠BMD,
∴∠AMD=∠AMB-∠BMD=∠BMF-∠CMB=∠CMF,
即:∠AMD=∠FMC.
点评 此题考查了圆周角定理以及垂径定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
13.分式:①$\frac{x+1}{{{x^2}+1}}$;②$\frac{a-b}{{{a^2}-{b^2}}}$;③$\frac{4a}{12(a-b)}$;④$\frac{1}{x-2}$中,最简分式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.方程x2-4x+4=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
8.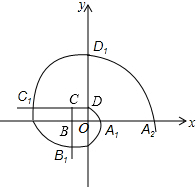 如图,边长为1正方形OBCD的顶点O在坐标原点,点B,D分别在x轴,y轴上,点C在第二象限,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中$\widehat{D{A}_{1}}$,$\widehat{{A}_{1}{B}_{1}}$,$\widehat{{B}_{1}{C}_{1}}$,$\widehat{{C}_{1}{D}_{1}}$,…,的圆心依次按O,B,C,D循环,则点B5的坐标为( )
如图,边长为1正方形OBCD的顶点O在坐标原点,点B,D分别在x轴,y轴上,点C在第二象限,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中$\widehat{D{A}_{1}}$,$\widehat{{A}_{1}{B}_{1}}$,$\widehat{{B}_{1}{C}_{1}}$,$\widehat{{C}_{1}{D}_{1}}$,…,的圆心依次按O,B,C,D循环,则点B5的坐标为( )
 如图,边长为1正方形OBCD的顶点O在坐标原点,点B,D分别在x轴,y轴上,点C在第二象限,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中$\widehat{D{A}_{1}}$,$\widehat{{A}_{1}{B}_{1}}$,$\widehat{{B}_{1}{C}_{1}}$,$\widehat{{C}_{1}{D}_{1}}$,…,的圆心依次按O,B,C,D循环,则点B5的坐标为( )
如图,边长为1正方形OBCD的顶点O在坐标原点,点B,D分别在x轴,y轴上,点C在第二象限,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中$\widehat{D{A}_{1}}$,$\widehat{{A}_{1}{B}_{1}}$,$\widehat{{B}_{1}{C}_{1}}$,$\widehat{{C}_{1}{D}_{1}}$,…,的圆心依次按O,B,C,D循环,则点B5的坐标为( )| A. | (-1,-5) | B. | (-1,-18) | C. | (-1,-14) | D. | (-18,-1) |
15.一元二次方程x2-3x-7=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 有一个实数根 |
12.A、B两地相距80千米,一辆大汽车从A地开出2小时后,又从A地开出另一辆小汽车,已知小汽车的速度是大汽车速度的3倍,结果小汽车比大汽车早40分钟到达B地,求两种汽车每小时各走多少千米.设大汽车的速度为xkm/h,则下面所列方程正确的是( )
| A. | $\frac{80}{x}$-$\frac{80}{3x}$=40 | B. | $\frac{80}{x}$-$\frac{80}{3x}$=2.4 | C. | $\frac{80}{x}$-2=$\frac{80}{3x}$+$\frac{2}{3}$ | D. | $\frac{80}{x}$+2=$\frac{80}{3x}$-$\frac{2}{3}$ |
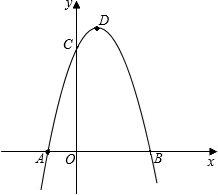 如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.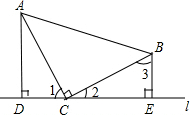 如图,在△ABC中,∠ACB=90°,CA=BC,直线l在△ABC的外部且过点C,AD⊥l,BE⊥l,垂足分别为点D、E.
如图,在△ABC中,∠ACB=90°,CA=BC,直线l在△ABC的外部且过点C,AD⊥l,BE⊥l,垂足分别为点D、E.