题目内容
13.分式:①$\frac{x+1}{{{x^2}+1}}$;②$\frac{a-b}{{{a^2}-{b^2}}}$;③$\frac{4a}{12(a-b)}$;④$\frac{1}{x-2}$中,最简分式有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 最简分式的标准是分子,分母中不含有公因式,不能再约分.判断的方法是把分子、分母分解因式,并且观察有无互为相反数的因式,这样的因式可以通过符号变化化为相同的因式从而进行约分.
解答 解:①$\frac{x+1}{{{x^2}+1}}$是最简分式;
②$\frac{a-b}{{{a^2}-{b^2}}}$=$\frac{a-b}{(a+b)(a-b)}$=$\frac{1}{a+b}$,不是最简分式;
③$\frac{4a}{12(a-b)}$=$\frac{a}{3(a-b)}$,不是最简分式;
④$\frac{1}{x-2}$是最简分式;
最简分式有①④,共2个;
故选B.
点评 此题考查了最简分式,分式的化简过程,首先要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.

练习册系列答案
相关题目
4.下列事件是必然事件的是( )
| A. | 太阳从西方升起 | |
| B. | 若a<0,则|a|=-a | |
| C. | 打开电视正在播放动画片《喜羊羊与灰太狼》 | |
| D. | 某运动员投篮时连续3次全中 |
18.下列长度的3条线段,能构成三角形的是( )
| A. | 1cm,4cm,3cm | B. | 2cm,3cm,4cm | C. | 4cm,4cm,8cm | D. | 5cm,6cm,12cm |
5.下面计算正确的是( )
| A. | 3+$\sqrt{3}$=3$\sqrt{3}$ | B. | $\sqrt{12}$÷$\sqrt{3}$=2 | C. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{(-6)^{2}}$=-6 |
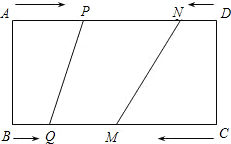 如图所示,在长方形ABCD中,BC=24cm,AB=10cm,点P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在长方形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.
如图所示,在长方形ABCD中,BC=24cm,AB=10cm,点P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在长方形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.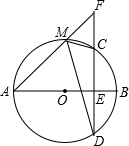 已知:如图,AB是⊙O的直径,CD为弦,且AB⊥CD于E,F为DC延长线上一点,连结AF交⊙O于M.
已知:如图,AB是⊙O的直径,CD为弦,且AB⊥CD于E,F为DC延长线上一点,连结AF交⊙O于M.