��Ŀ����
11��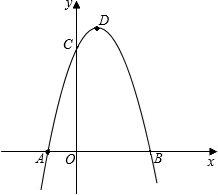 ��ͼ��������y=-x2+2x+3��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪD��
��ͼ��������y=-x2+2x+3��x���ཻ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪD����1��ֱ��д��A��B��C���������������ߵĶԳ��
��2������BC���������ߵĶԳ��ύ�ڵ�E����PΪ�߶�BC�ϵ�һ�����㣬����P��PF��DE���������ڵ�F�����P�ĺ�����Ϊm��
���ú�m�Ĵ���ʽ��ʾ�߶�PF�ij����������mΪ��ֵʱ���ı���PEDFΪƽ���ı��Σ�
�����BCF�����ΪS����S��m�ĺ�����ϵʽ��
��3�������������Ƿ���ڵ�G��ʹ��DGBΪֱ�������Σ������ڣ���ֱ��д��G������ꣻ�������ڣ���˵�����ɣ�
���� ��1����֪�������ߵĽ���ʽ����y=0ʱ�����A��B��������꣬��x=0ʱ�������C������꣮���ݶԳ���x=-$\frac{b}{2a}$�ɵó��Գ���Ľ���ʽ��
��2��PF�ij����ǵ�x=mʱ�������ߵ�ֵ��ֱ��BC����һ�κ�����ֵ�IJ���ȸ���B��C���������BC����ֱ�ߵĽ���ʽ��Ȼ��m�ֱ����ֱ��BC�������ߵĽ���ʽ�У��ó���������ֵ�IJ����PF�ij�������ֱ��BC�Ľ���ʽ���ɵó�E������꣬���������ߵĽ���ʽ�����D������꣬Ȼ���������ϵ������ľ��빫ʽ�������DE�ij���Ȼ����PF=DE�����������ʱm��ֵ��
��3���ɽ�������BCF�ֳ�����������
һ������������PFC����PFΪ�ױߣ���P�ĺ�����Ϊ���ɵó�������PFC�������
һ������������PFB����PFΪ�ױߣ���P��B����ĺ������ľ���ֵΪ�ߣ��������������PFB�������
Ȼ�����������BCF�����=������PFC�����+������PFB����������������S��m�ĺ�����ϵʽ��
��� �⣺��1����y=0����-x2+2x+3=-��x+1����x-3��=0��
���x=-1��x=3����A��-1��0����B��3��0����
�����ߵĶԳ����ǣ�ֱ��x=1��
��x=0����y=0����C��0��3����
����������A��-1��0����B��3��0����C��0��3���������ߵĶԳ�����x=1��
��2������ֱ��BC�ĺ�����ϵʽΪ��y=kx+b��
��B��3��0����C��0��3���ֱ����ã�$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$��
����ֱ��BC�ĺ�����ϵʽΪ��y=-x+3��
��x=1ʱ��y=-1+3=2��
��E��1��2����
��x=mʱ��y=-m+3��
��P��m��-m+3����
��y=-x2+2x+3�У���x=1ʱ��y=4��
��D��1��4��
��x=mʱ��y=-m2+2m+3��
��F��m��-m2+2m+3��
���߶�DE=4-2=2��
�߶�PF=-m2+2m+3-��-m+3��=-m2+3m
��PF��DE��
�൱PF=EDʱ���ı���PEDFΪƽ���ı��Σ�
��-m2+3m=2��
��ã�m1=2��m2=1���������⣬��ȥ����
��ˣ���m=2ʱ���ı���PEDFΪƽ���ı��Σ�
����ֱ��PF��x�ύ�ڵ�M����B��3��0����O��0��0����
�ɵã�OB=OM+MB=3��
��S=S��BPF+S��CPF
��S=$\frac{1}{2}$PF•BM+$\frac{1}{2}$PF•OM=$\frac{1}{2}$PF•��BM+OM��=$\frac{1}{2}$PF•OB��
��S=$\frac{1}{2}$��3��-m2+3m��=-$\frac{3}{2}$m2+$\frac{9}{2}$m��0��m��3����
��3���ߵ�B��3��0����D��1��4����
��ֱ��BD�Ľ���ʽΪy=-2x+6��
����BDΪֱ�DZ���BΪ����ʱ����ֱ��BG1�Ľ���ʽΪy=$\frac{1}{2}$x+b��
�߾���B��3��0����
��ֱ��BG1�Ľ���ʽΪy=$\frac{1}{2}$x-$\frac{3}{2}$��
��$\frac{1}{2}$x-$\frac{3}{2}$=-x2+2x+3��
��ã�x=-$\frac{3}{2}$��x=3����ȥ����
��x=-$\frac{3}{2}$����y=-x2+2x+3��y=-$\frac{9}{4}$��
��G1��������-$\frac{3}{2}$��-$\frac{9}{4}$����
����BDΪֱ�DZ���DΪ����ʱ����ֱ��BG2�Ľ���ʽΪy=$\frac{1}{2}$x+b��
�߾���D��1��4����
��ֱ��BG2�Ľ���ʽΪy=$\frac{1}{2}$x+$\frac{7}{2}$��
��$\frac{1}{2}$x+$\frac{7}{2}$=-x2+2x+3��
��ã�x=$\frac{1}{2}$��x=1����ȥ����
��x=$\frac{1}{2}$����y=-x2+2x+3��y=$\frac{15}{4}$��
��G2��������$\frac{1}{2}$��$\frac{15}{4}$����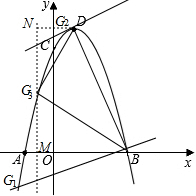
����BDΪб��ʱ����G3������Ϊ��x��-x2+2x+3����
��ͼ����BM=3-x��G3M=-x2+2x+3��NG3=4-��-x2+2x+3��=x2-2x+1��DN=1-x��
��BG32+G3D2=BD2��
����BM2+G3M2+NG32+DN2=BD2��
�ࣨ3-x��2+��-x2+2x+3��2+��x2-2x+1��2+��1-x��2=20��
��ã�x=1��3������ȥ����
���ϣ���G������Ϊ��-$\frac{3}{2}$��-$\frac{9}{4}$������$\frac{1}{2}$��$\frac{15}{4}$������0��3����
���� ������Ҫ�����˶��κ������ۺ�Ӧ�ã����ݶ��κ����ó���ص������ͶԳ���Ľ���ʽ�ǽ���Ļ�����

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�| A�� | $\frac{1}{4}$ | B�� | $\frac{3}{4}$ | C�� | $\frac{7}{4}$ | D�� | $\frac{4}{7}$ |
| A�� | $\sqrt{2}$cm | B�� | $\sqrt{3}$cm | C�� | 3cm | D�� | $\sqrt{5}$cm |
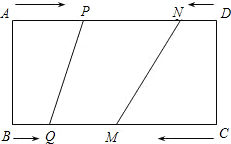 ��ͼ��ʾ���ڳ�����ABCD�У�BC=24cm��AB=10cm����P��Q��M��N�ֱ��A��B��C��D������AD��BC��CB��DA�����ڳ����εı���ͬʱ�˶�������һ�����ȵ��������˶��ߵ���һ���˵�ʱ���˶���ֹͣ����֪����ͬʱ���ڣ���BQ=xcm��x��0������AP=2xcm��CM=3xcm��DN=x2cm��
��ͼ��ʾ���ڳ�����ABCD�У�BC=24cm��AB=10cm����P��Q��M��N�ֱ��A��B��C��D������AD��BC��CB��DA�����ڳ����εı���ͬʱ�˶�������һ�����ȵ��������˶��ߵ���һ���˵�ʱ���˶���ֹͣ����֪����ͬʱ���ڣ���BQ=xcm��x��0������AP=2xcm��CM=3xcm��DN=x2cm��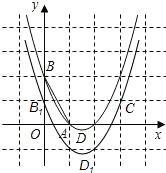 ��ͼ����֪������y=x2+bx+c����A��1��0����B��0��2�����㣬����ΪD������OAB�Ƶ�A˳ʱ����ת90���B�䵽��C��λ�ã�����������y��ƽ�ƺ���C��������������y��Ľ���ΪB1������ΪD1������N��ƽ�ƺ���������ϣ��������NBB1������ǡ�NDD1�����2�������N������Ϊ��1��-1������3��1����
��ͼ����֪������y=x2+bx+c����A��1��0����B��0��2�����㣬����ΪD������OAB�Ƶ�A˳ʱ����ת90���B�䵽��C��λ�ã�����������y��ƽ�ƺ���C��������������y��Ľ���ΪB1������ΪD1������N��ƽ�ƺ���������ϣ��������NBB1������ǡ�NDD1�����2�������N������Ϊ��1��-1������3��1����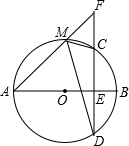 ��֪����ͼ��AB�ǡ�O��ֱ����CDΪ�ң���AB��CD��E��FΪDC�ӳ�����һ�㣬����AF����O��M��
��֪����ͼ��AB�ǡ�O��ֱ����CDΪ�ң���AB��CD��E��FΪDC�ӳ�����һ�㣬����AF����O��M��