题目内容
15.学校有一块正方形花坛,面积为15cm2,求它的对角线长.分析 设正方形的边长为xcm,由题意得出x2=15,根据勾股定理得出正方形的对角线长=$\sqrt{{x}^{2}+{x}^{2}}$=$\sqrt{30}$(cm)即可.
解答 解:设正方形的边长为xcm,
根据题意得:x2=15,
根据勾股定理得:正方形的对角线长=$\sqrt{{x}^{2}+{x}^{2}}$=$\sqrt{15+15}$=$\sqrt{30}$(cm);
答:正方形的对角线长为$\sqrt{30}$cm.
点评 本题考查了正方形的性质、勾股定理;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.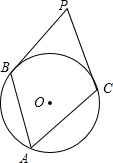 如图,圆周角∠BAC=55°,分别过B、C两点作⊙O的切线相交于P,则∠BPC为( )
如图,圆周角∠BAC=55°,分别过B、C两点作⊙O的切线相交于P,则∠BPC为( )
 如图,圆周角∠BAC=55°,分别过B、C两点作⊙O的切线相交于P,则∠BPC为( )
如图,圆周角∠BAC=55°,分别过B、C两点作⊙O的切线相交于P,则∠BPC为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
3.计算a2-(a+b)2的结果是( )
| A. | 2ab+b2 | B. | -2ab-b2 | C. | 2a2+2ab+b2 | D. | 非上述答案 |
7. 如图是一个三棱柱的展开图,若AD=13,CD=3,则AB的长度不可能是( )
如图是一个三棱柱的展开图,若AD=13,CD=3,则AB的长度不可能是( )
 如图是一个三棱柱的展开图,若AD=13,CD=3,则AB的长度不可能是( )
如图是一个三棱柱的展开图,若AD=13,CD=3,则AB的长度不可能是( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
5.-$\frac{1}{2}$的相反数是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | ±$\frac{1}{2}$ |
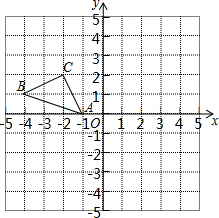 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: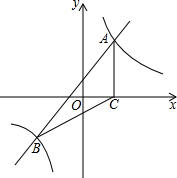 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点