题目内容
20.2016年中国移动推出“自由派”资费套餐,其计费方式有两种如下表:| 月租费/元 | 区内主叫全国时长/分钟 | 超套主叫费/(元/分钟) | 被叫 | |
| 方式一 | 9 | 50 | 0.2 | 免费 |
| 方式二 | 19 | 130 | 0.15 | 免费 |
(1)如果甲平均每月的通话时长为80分钟,乙平均每月的通话时长为200分钟,请你通过计算说明:甲、乙分别选择哪种计费方式省钱;
(2)设某人一个月内用移动电话主叫时长为t分钟(t是正整数).请你为用户设计一个方案,使用户能合理地选择这种资费套餐的计费方式.
分析 (1)分别求出通话时长为80分钟与200分钟时,选择方式一与方式二计费的费用,再比较即可;
(2)分三种情况讨论:①t≤50; ②50<t<130;③t≥130.
解答 解:(1)当通话时间为80分钟时,
若用方式一计费,则费用为:9+(80-50)×0.2=15,
若用方式二计费,则费用为:19,
因为15<19,
此时甲选择方式一省钱;
当通话时间为200分钟时,
若用方式一计费,则费用为:9+(200-50)×0.2=39,
若用方式二计费,则费用为:19+(200-130)×0.15=29.5,
因为29.5<39,
此时乙选择方式二省钱;
(2)若设一个月内用移动电话主叫时长为t分钟(t是正整数).则根据题意可得
①当t≤50时,按方式一计费省钱;
②当50<t<130时,
令9+0.2 (t-50)=19,
解得:t=100.
则:当50<t<100时,方式一比方式二的费用少;
当t=100时,方式一与方式二的费用相等;
当100<t<130时,方式一比方式二的费用多;
③当t≥130时,
方式一计费为:9+0.2 (t-50)=0.2t-1,
方式二计费为:19+0.15 (t-130)=0.15t-0.5,
因为此时方式一的单位时间的费用0.2比方式二的单位时间的费用0.15大,所以此时方式二计费少.
综上分析,可得到:
当0≤t<100时,选择方式一省钱;
当t=100时,选择方式一与方式二均可;
当t>100时,选择方式二省钱.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,理解两种计费方式,进行正确分类讨论.

练习册系列答案
相关题目
1.若a2=16,$\root{3}{b}$=-2,则a+b=( )
| A. | -4 | B. | -12 | C. | -4或-12 | D. | ±4或±12 |
11.函数y=(2m-1)x${\;}^{{m}^{2}-2}$是反比例函数,在第一象限内y随x的增大而减小,则m=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | ±$\sqrt{3}$ |
15.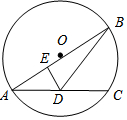 如图,AB是⊙O的直径,AC是⊙O的弦,D是AC的中点,过D作DE⊥AB于点E,连结BD.若AD=5,AE=4,则BD的长为( )
如图,AB是⊙O的直径,AC是⊙O的弦,D是AC的中点,过D作DE⊥AB于点E,连结BD.若AD=5,AE=4,则BD的长为( )
 如图,AB是⊙O的直径,AC是⊙O的弦,D是AC的中点,过D作DE⊥AB于点E,连结BD.若AD=5,AE=4,则BD的长为( )
如图,AB是⊙O的直径,AC是⊙O的弦,D是AC的中点,过D作DE⊥AB于点E,连结BD.若AD=5,AE=4,则BD的长为( )| A. | 2$\sqrt{15}$ | B. | $\sqrt{35}$ | C. | $\frac{5}{2}$$\sqrt{13}$ | D. | $\frac{7}{2}$$\sqrt{7}$ |
5.下列图形中,是轴对称图形的为( )
| A. |  | B. |  | C. |  | D. |  |
12.下列命题中的真命题是( )
| A. | 两个直角三角形都相似 | |
| B. | 一个直角三角形的两条边和另一个直角三角形的两条边成比例,那么这两个直角三角形相似 | |
| C. | 两个等腰三角形都相似 | |
| D. | 两个等腰直角三角形都相似 |