题目内容
19.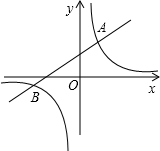 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4)
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4)(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标.
分析 (1)把A点坐标代入反比例函数解析式可求得k的值,可求得反比例函数解析式和A点坐标,把A点坐标代入一次函数可求得b的值,可求得一次函数表达式;
(2)联立两函数解析式,求方程的解可求得B点坐标.
解答 解:(1)把A点坐标代入反比例函数解析式可得-k+4=k,解得k=2,
∴反比例函数解析式为y=$\frac{2}{x}$,且A点坐标为(1,2),
∵A点在一次函数图象上,
∴2=1+b,解得b=1,
∴一次函数解析式为y=x+1,
(2)联立两函数解析式可得$\left\{\begin{array}{l}{y=\frac{2}{x}}\\{y=x+1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$,
∴B点坐标为(-2,-1).
点评 本题主要考查函数图象的交点,掌握函数图象的交点坐标满足两函数解析式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )
如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )
 如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )
如图,用宽度都是2的矩形纸带叠放成一个锐角为60°的四边形,则此四边形的面积S为( )| A. | 4 | B. | $\frac{4}{3}$$\sqrt{3}$ | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | $\frac{8}{3}$$\sqrt{3}$ |
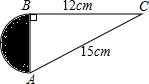 求阴影部分的面积.
求阴影部分的面积.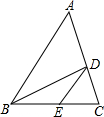 如图,△ABC中,CE:EB=2:3,DE∥AB,若△ABC的面积为25,则△BDE的面积为6.
如图,△ABC中,CE:EB=2:3,DE∥AB,若△ABC的面积为25,则△BDE的面积为6. 已知,点E是AB的中点,AF=BD,BD=5,AC=7,求DC.
已知,点E是AB的中点,AF=BD,BD=5,AC=7,求DC. 如图,⊙O的半径为10,A、B、C是圆周上三点,∠BAC=36°,则劣弧BC的长是4π.
如图,⊙O的半径为10,A、B、C是圆周上三点,∠BAC=36°,则劣弧BC的长是4π.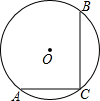 如图,在⊙O中,弦AC⊥BC,若AC=6cm,BC=8cm,则⊙O的半径为5cm.
如图,在⊙O中,弦AC⊥BC,若AC=6cm,BC=8cm,则⊙O的半径为5cm.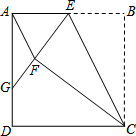 如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G.
如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G.