题目内容
1.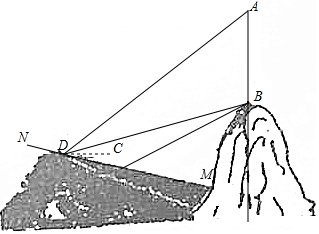 如图所示.在山顶上有一座电视塔AB(AB与水平面垂直),小明同学要测量电视塔AB的高度,在斜坡MN上取一点C,测得塔底B的仰角为30°,坡底M的俯角为15°,小明沿斜坡MN上行20米到点D,在点D测得塔底B的仰角为15°,塔顶A的仰角为45°,请根据以上数据帮助小明求出电视塔AB的高度(结果保留根号).
如图所示.在山顶上有一座电视塔AB(AB与水平面垂直),小明同学要测量电视塔AB的高度,在斜坡MN上取一点C,测得塔底B的仰角为30°,坡底M的俯角为15°,小明沿斜坡MN上行20米到点D,在点D测得塔底B的仰角为15°,塔顶A的仰角为45°,请根据以上数据帮助小明求出电视塔AB的高度(结果保留根号).
分析 先过D作DF⊥AB于F,过B作BE⊥DC于E,过B作BG⊥AD,设BE=CE=x,根据DE=20+x,DE=$\sqrt{3}$BE=$\sqrt{3}$x,可得方程20+x=$\sqrt{3}$x,求得BE=10$\sqrt{3}$+10,进而得到BG=BE=10$\sqrt{3}$+10,最后根据△ABG是等腰直角三角形,即可得出AB=$\sqrt{2}$BG=10$\sqrt{6}$+10$\sqrt{2}$.
解答  解:如图所示,过D作DF⊥AB于F,过B作BE⊥DC于E,过B作BG⊥AD,
解:如图所示,过D作DF⊥AB于F,过B作BE⊥DC于E,过B作BG⊥AD,
由题可得,∠BCE=30°+15°=45°,则△BCE是等腰直角三角形,
设BE=CE=x,则DE=20+x,
∵∠BDE=15°+15°=30°,
∴tan∠BDE=$\frac{BE}{DE}$=$\frac{\sqrt{3}}{3}$,
即DE=$\sqrt{3}$BE=$\sqrt{3}$x,
∴20+x=$\sqrt{3}$x,
解得x=10$\sqrt{3}$+10,
即BE=10$\sqrt{3}$+10,
又∵∠ADB=∠ADF-∠BDF=45°-15°=30°,∠BDE=30°,
∴BD平分∠ADC,
∴BG=BE=10$\sqrt{3}$+10,
又∵∠ADF=45°,
∴∠A=45°,
即△ABG是等腰直角三角形,
∴AB=$\sqrt{2}$BG=$\sqrt{2}$(10$\sqrt{3}$+10)=10$\sqrt{6}$+10$\sqrt{2}$,
故电视塔AB的高度为(10$\sqrt{6}$+10$\sqrt{2}$)米.
点评 本题考查解直角三角形-仰角问题、锐角三角函数、勾股定理等知识的综合应用,解题的关键是依据特殊角添加常用辅助线,构造特殊的直角三角形解决问题.

| A. | a≤0 | B. | a<0 | C. | 0<a<2 | D. | a≤0或a=2 |
| A. | 2 | B. | $\sqrt{5}$+1 | C. | 2或$\sqrt{5}$+1 | D. | 以上都不对 |
| A. | -5≤x0-3 | B. | -5≤x0<2 | C. | x0≥-5 | D. | -5≤x0<-1 |
 已知一次函数y=kx+b的图象如图所示,则当x<1时,y的取值范围是( )
已知一次函数y=kx+b的图象如图所示,则当x<1时,y的取值范围是( )| A. | y<-4 | B. | y<-2 | C. | -2<y<0 | D. | -4<y<0 |
| A. | 3 | B. | 5 | C. | -3 | D. | -5 |
 如图,多边形的相邻两边均互相垂直,则这个多边形的周长为2a+2b.
如图,多边形的相邻两边均互相垂直,则这个多边形的周长为2a+2b.