题目内容
4.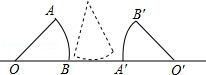 如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是$\frac{4}{3}$π.
如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是$\frac{4}{3}$π.
分析 仔细观察顶点O经过的路线可得,顶点O到O′所经过的路线可以分为三段,分别求出三段的长,再求出其和即可.
解答 解:顶点O经过的路线可以分为三段,当弧AB切直线l于点B时,有OB⊥直线l,此时O点绕不动点B转过了90°;
第二段:OB⊥直线l到OA⊥直线l,O点绕动点转动,而这一过程中弧AB始终是切于直线l的,所以O与转动点的连线始终⊥直线l,所以O点在水平运动,此时O点经过的路线长=BA′=AB的弧长;
第三段:OA⊥直线l到O点落在直线l上,O点绕不动点A转过了90°.
所以,O点经过的路线总长S=$\frac{1}{2}$π+$\frac{1}{3}$π+$\frac{1}{2}$π=$\frac{4}{3}$π.
故答案是:$\frac{4}{3}π$.
点评 本题考查了旋转的性质,弧长的计算,根据题意,准确分析得到三段的运动过程是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
14.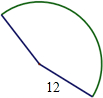 如图,用半径为12cm,面积72πcm2的扇形无重叠地围成一个圆锥,则这个圆锥的高为( )
如图,用半径为12cm,面积72πcm2的扇形无重叠地围成一个圆锥,则这个圆锥的高为( )
 如图,用半径为12cm,面积72πcm2的扇形无重叠地围成一个圆锥,则这个圆锥的高为( )
如图,用半径为12cm,面积72πcm2的扇形无重叠地围成一个圆锥,则这个圆锥的高为( )| A. | 12cm | B. | 6cm | C. | 6$\sqrt{2}$cm | D. | 6$\sqrt{3}$cm |
13.下列命题中正确的是( )
| A. | 平分弦的直径垂直于这条弦 | |
| B. | 切线垂直于圆的半径 | |
| C. | 三角形的外心到三角形三边的距离相等 | |
| D. | 圆内接平行四边形是矩形 |
14. 如图,已知∠A=33°,∠B=75°,点C在直线AD上,则∠BCD为( )
如图,已知∠A=33°,∠B=75°,点C在直线AD上,则∠BCD为( )
 如图,已知∠A=33°,∠B=75°,点C在直线AD上,则∠BCD为( )
如图,已知∠A=33°,∠B=75°,点C在直线AD上,则∠BCD为( )| A. | 147° | B. | 108° | C. | 105° | D. | 以上答案都不对 |
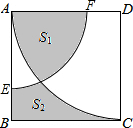 如图,在边长为4的正方形ABCD中,以A为圆心,3为半径作圆弧$\widehat{EF}$,以D为圆心,4为半径作圆弧$\widehat{AC}$.若图中阴影部分的面积分别为S1,S2,则S1-S2=$\frac{25π}{4}$-16.
如图,在边长为4的正方形ABCD中,以A为圆心,3为半径作圆弧$\widehat{EF}$,以D为圆心,4为半径作圆弧$\widehat{AC}$.若图中阴影部分的面积分别为S1,S2,则S1-S2=$\frac{25π}{4}$-16.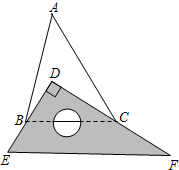 已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,D、F恰好分别经过点B、C.
已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,D、F恰好分别经过点B、C. 如图,点B(2,2)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{3}{x}$(x<0)上,点A、C分别在x轴、y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
如图,点B(2,2)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{3}{x}$(x<0)上,点A、C分别在x轴、y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.