题目内容
14.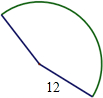 如图,用半径为12cm,面积72πcm2的扇形无重叠地围成一个圆锥,则这个圆锥的高为( )
如图,用半径为12cm,面积72πcm2的扇形无重叠地围成一个圆锥,则这个圆锥的高为( )| A. | 12cm | B. | 6cm | C. | 6$\sqrt{2}$cm | D. | 6$\sqrt{3}$cm |
分析 先根据扇形的面积公式计算出扇形的圆心角,再利用周长公式计算出底面圆的周长,得出半径.再构建直角三角形,解直角三角形即可.
解答 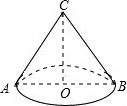 解:72π=$\frac{nπ×1{2}^{2}}{360}$
解:72π=$\frac{nπ×1{2}^{2}}{360}$
解得n=180°,
∴扇形的弧长=$\frac{180π×12}{180}$=12πcm.
围成一个圆锥后如图所示:
因为扇形弧长=圆锥底面周长
即12π=2πr
解得r=6cm,即OB=6cm
根据勾股定理得OC=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$cm,
故选D.
点评 本题综合考查了弧长公式,扇形弧长=用它围成的圆锥底面周长,及勾股定理等知识,所以学生学过的知识一定要结合起来.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
5.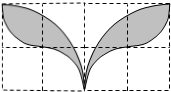 如图,小方格都是边长为1的正方形,则以格点为圆心,半径分别为1和2的两种弧围成的“叶状”阴影图案的面积为( )
如图,小方格都是边长为1的正方形,则以格点为圆心,半径分别为1和2的两种弧围成的“叶状”阴影图案的面积为( )
 如图,小方格都是边长为1的正方形,则以格点为圆心,半径分别为1和2的两种弧围成的“叶状”阴影图案的面积为( )
如图,小方格都是边长为1的正方形,则以格点为圆心,半径分别为1和2的两种弧围成的“叶状”阴影图案的面积为( )| A. | π-2 | B. | 2π-4 | C. | 4π-4 | D. | 4π-8 |
19.在?ABCD中,∠A:∠B:∠C:∠D的值可能是( )
| A. | 3:4:4:5 | B. | 2:5:2:5 | C. | 4:4:3:2 | D. | 2:3:5:6 |
6. 如图,字母B所代表的正方形的面积是( )
如图,字母B所代表的正方形的面积是( )
 如图,字母B所代表的正方形的面积是( )
如图,字母B所代表的正方形的面积是( )| A. | 144 | B. | 194 | C. | 12 | D. | 169 |
 如图所示,直线AB,CD,EF相交于点O,则∠AOD的对顶角是∠BOC.
如图所示,直线AB,CD,EF相交于点O,则∠AOD的对顶角是∠BOC. 将一副三角板拼成如图所示的图案,则∠ACD的度数为105°.
将一副三角板拼成如图所示的图案,则∠ACD的度数为105°.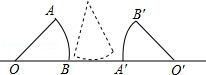 如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是$\frac{4}{3}$π.
如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是$\frac{4}{3}$π.