题目内容
9.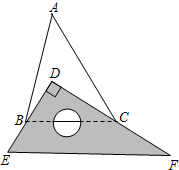 已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,D、F恰好分别经过点B、C.
已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,D、F恰好分别经过点B、C.(1)∠DBC+∠DCB=90度;
(2)试说明:∠ABD+∠ACD=90°-∠A.
分析 (1)在△DBC中,根据三角形内角和定理得∠DBC+∠DCB+∠D=180°,然后把∠D=90°代入计算即可;
(2)在Rt△ABC中,根据三角形内角和定理得∠ABC+∠ACB+∠A=180°,即∠ABD+∠DBC+∠DCB+∠ACD+∠A=180°,然后把(1)中的结论代入计算即可.
解答 解:(1)在△DBC中,∵∠DBC+∠DCB+∠D=180°,
而∠D=90°,
∴∠DBC+∠DCB=90°;
故答案为90;
(2)在Rt△ABC中,
∵∠ABC+∠ACB+∠A=180°,
即∠ABD+∠DBC+∠DCB+∠ACD+∠A=180°,
而∠DBC+∠DCB=90°,
∴∠ABD+∠ACD=90°-∠A.
点评 本题考查了三角形内角和定理:三角形内角和是180°.准确识别图性是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.在?ABCD中,∠A:∠B:∠C:∠D的值可能是( )
| A. | 3:4:4:5 | B. | 2:5:2:5 | C. | 4:4:3:2 | D. | 2:3:5:6 |
1.下列四个数中最大的数是( )
| A. | 2015+(-2014) | B. | 2015×(-2014) | C. | 2015-2014 | D. | (-2014)2015 |
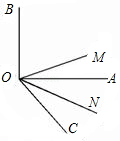 如图,∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC.∠AOC=50°,求∠MON的度数.
如图,∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC.∠AOC=50°,求∠MON的度数.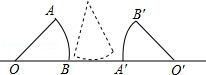 如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是$\frac{4}{3}$π.
如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是$\frac{4}{3}$π.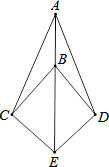 如图,点B在线段AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:EC=ED.
如图,点B在线段AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:EC=ED.