题目内容
16. 如图,点B(2,2)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{3}{x}$(x<0)上,点A、C分别在x轴、y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
如图,点B(2,2)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{3}{x}$(x<0)上,点A、C分别在x轴、y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.(1)求k的值;
(2)求点A的坐标.
分析 (1)把B的坐标代入求出即可;
(2)设MD=a,OM=b,求出ab=3,过D作DM⊥x轴于M,过B作BN⊥x轴于N,证△ADM≌△BAN,推出BN=AM=2,MD=AN=a,求出a=b,求出a的值即可.
解答 解:(1)∵B(2,2)在双曲线y=$\frac{k}{x}$上,
∴k=2×2=4;
(2)如图,过D作DM⊥x轴于M,过B作BN⊥x轴于N,
∵B(2,2),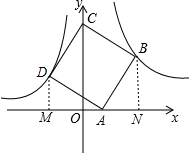
∴BN=ON=2,
设MD=a,OM=b,
∵D在双曲线y=-$\frac{3}{x}$(x<0)上,
∴ab=3,
∵四边形ABCD是正方形,
∴∠DAB=90°,AD=AB,
∴∠MDA+∠DAM=90°,∠DAM+∠BAN=90°,
∴∠ADM=∠BAN,
在△ADM和△BAN中,
$\left\{\begin{array}{l}{∠MDA=∠NAB}\\{∠DMA=∠ANB}\\{AD=BA}\end{array}\right.$,
∴△ADM≌△BAN(AAS),
∴BN=AM=2,DM=AN=a,
∴0A=2-a,
即AM=b+2-a=2,
a=b,
∵ab=3,
∴a=b=$\sqrt{3}$,
∴OA=2-$\sqrt{3}$,
即点A的坐标是(2-$\sqrt{3}$,0).
点评 本题考查了正方形的性质,反比例函数图象上点的坐标特征,全等三角形的性质和判定的应用,作出辅助线构建全等三角形是本题的关键.

练习册系列答案
相关题目
5.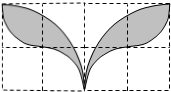 如图,小方格都是边长为1的正方形,则以格点为圆心,半径分别为1和2的两种弧围成的“叶状”阴影图案的面积为( )
如图,小方格都是边长为1的正方形,则以格点为圆心,半径分别为1和2的两种弧围成的“叶状”阴影图案的面积为( )
 如图,小方格都是边长为1的正方形,则以格点为圆心,半径分别为1和2的两种弧围成的“叶状”阴影图案的面积为( )
如图,小方格都是边长为1的正方形,则以格点为圆心,半径分别为1和2的两种弧围成的“叶状”阴影图案的面积为( )| A. | π-2 | B. | 2π-4 | C. | 4π-4 | D. | 4π-8 |
6. 如图,字母B所代表的正方形的面积是( )
如图,字母B所代表的正方形的面积是( )
 如图,字母B所代表的正方形的面积是( )
如图,字母B所代表的正方形的面积是( )| A. | 144 | B. | 194 | C. | 12 | D. | 169 |
1.下列四个数中最大的数是( )
| A. | 2015+(-2014) | B. | 2015×(-2014) | C. | 2015-2014 | D. | (-2014)2015 |
8.下列选项中,说法错误的是:1是-1的( )
| A. | 相反数 | B. | 绝对值 | C. | 倒数 | D. | 平方 |
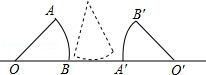 如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是$\frac{4}{3}$π.
如图所示,半径为1的圆心角为60°的扇形纸片OAB在直线L上向右做无滑动的滚动.且滚动至扇形O′A′B′处,则顶点O所经过的路线总长是$\frac{4}{3}$π.