题目内容
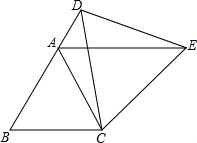 如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE.
如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边三角形CDE,连接AE.(1)求证:△CBD≌△CAE.
(2)判断AE与BC的位置关系,并说明理由.
考点:全等三角形的判定与性质,平行线的判定,等边三角形的性质
专题:
分析:(1)根据等边三角形各内角为60°和各边长相等的性质可证∠ECA=∠DCB,AC=BC,EC=DC,即可证明△ECA≌△DCB;
(2)根据△ECA≌△DCB可得∠EAC=60°,根据内错角相等,平行线平行即可解题.
(2)根据△ECA≌△DCB可得∠EAC=60°,根据内错角相等,平行线平行即可解题.
解答:证明:(1)∵△ABC、△DCE为等边三角形,
∴AC=BC,EC=DC,∠ACB=∠ECD=∠DBC=60°,
∵∠ACD+∠ACB=∠DCB,∠ECD+∠ACD=∠ECA,
∴∠ECA=∠DCB,
在△ECA和△DCB中,
,
∴△ECA≌△DCB(SAS);
(2)∵△ECA≌△DCB,
∴∠EAC=∠DBC=60°,
又∵∠ACB=∠DBC=60°,
∴∠EAC=∠ACB=60°,
∴AE∥BC.
∴AC=BC,EC=DC,∠ACB=∠ECD=∠DBC=60°,
∵∠ACD+∠ACB=∠DCB,∠ECD+∠ACD=∠ECA,
∴∠ECA=∠DCB,
在△ECA和△DCB中,
|
∴△ECA≌△DCB(SAS);
(2)∵△ECA≌△DCB,
∴∠EAC=∠DBC=60°,
又∵∠ACB=∠DBC=60°,
∴∠EAC=∠ACB=60°,
∴AE∥BC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ECA≌△DCB是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
多项式3x2-y+3xy3+x4-1的项和次数是( )
| A、3x2,y,3xy3,x4,1;次数是4 |
| B、3x2,-y,3xy3,x4,1;次数是4 |
| C、3x2,-y,3xy3,x4,-1;次数是4 |
| D、5;次数是4 |
已知线段AB=6,C是线段AB的中点,则线段AC长为( )
| A、6 | B、3 | C、3或6 | D、2 |
 如图,两个三角形通过适当摆放可摆成关于某条直线成轴对称图形,则x等于( )
如图,两个三角形通过适当摆放可摆成关于某条直线成轴对称图形,则x等于( )| A、50° | B、55° |
| C、75° | D、90° |

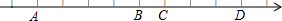 如图,数轴上标出若干个点,每相邻两点相距1个单位,点A,B,C,D对应的数分别是整数a,b,c,d,且b-2a=9,那么,这条数轴上的原点是( )
如图,数轴上标出若干个点,每相邻两点相距1个单位,点A,B,C,D对应的数分别是整数a,b,c,d,且b-2a=9,那么,这条数轴上的原点是( ) 在港口A的正西方向,有一观测点O,一条船从港口A出发,沿北偏东15°的方向航行到达B,从O点测得船位于北偏东60°的方向,OA=30km,求AB.
在港口A的正西方向,有一观测点O,一条船从港口A出发,沿北偏东15°的方向航行到达B,从O点测得船位于北偏东60°的方向,OA=30km,求AB.