题目内容
2.如图(1)所示,AB为⊙O直径,点C是弧AB的中点,动点D、E分别从点A、C同时出发,速度都是1个单位/秒,沿线段AC和CB移动,终点为C、B.设运动时间为x秒,△CDE的面积为y,已知y与x的函数图象是抛物线的一部分,如图(2)所示.连接OC,当OC=DE时,x=3.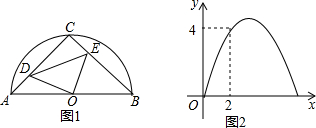
分析 由题意可以得出△ACB为等腰直角三角形,从而可将△CDE的面积用运动时间及AC的长表示出来,结合函数图象提供的数据求出AC的长,再利用勾股定理就能求出x的值了.
解答 解:∵AB为⊙O直径,点C是弧AB的中点,
∴∠C=90°,∠A=∠B=45°,
∴AC=BC,
∵设运动时间为x秒,
∴AD=x,CE=x,
∵设AC长为a,
∴DC=a-x,则y=$\frac{1}{2}$x(a-x),
∵由函数图象可知,当x=2时,y=4,
∴4=$\frac{1}{2}$×2×(a-2),解得a=6,
∴AB=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$
连接OC,如图所示:
∵∠C=90°,∠A=∠B=45°,
∴OC=$\frac{1}{2}$AB=3$\sqrt{2}$,
∴DE=OC=3$\sqrt{2}$
∴CD2+CE2=(3$\sqrt{2}$)2,即(6-x)2+x2=18,
解得x=3.
故答案为:3.
点评 本题考查了圆的性质、直角三角形性质、勾股定理及二次函数图象性质,解题的关键是由所给条件得出△ACB为等腰直角三角形,利用函数图象求出AC长,体现了数形结合的数学思想.

练习册系列答案
相关题目
12.有一组数据为88,96,109,109,122,141,则这组数据的众数和中位数分别是( )
| A. | 122,109 | B. | 109,122 | C. | 109,109 | D. | 141,109 |
13.计算(-4)+(-9)的结果是( )
| A. | -13 | B. | -5 | C. | 5 | D. | 13 |
7.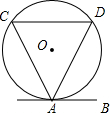 如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
 如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 5 | D. | 6 |
14.计算(-8)-(-5)的结果等于( )
| A. | -3 | B. | -13 | C. | -40 | D. | 3 |
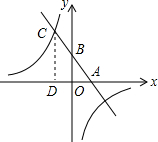 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6.