题目内容
16.甲、乙两人分别就角平分线的作法给出了不同的方法,甲:
(1)以点O为圆心,适当长为半径画弧,分别交OA、OB于点D,E;
(2)分别以点D,E为圆心,适当长为半径,在∠AOB内部画弧,两弧相交于点C;
(3)作射线OC,则OC为∠AOC的平分线
乙:
(1)以点O为圆心,任意长为半径画弧交OM、ON于点A、B;
(2)以点O为圆心,不等于(1)中的半径长为半径画弧交OM、ON于点C、D;
(3)连接AD、BD相交于点E;
(4)作射线OE,则OE为∠MON的平分线
( )
| A. | 甲对乙不对 | B. | 甲不对乙对 | C. | 甲乙都不对 | D. | 甲乙都对 |
分析 根据题目描述画出图形,甲的作法中证△ODC≌△OEC即可得;乙的作法中先证△AOD≌△BOC可得∠OAD=∠OBC,再证△ACE≌△BDE得CE=DE,最后证△OCE≌△ODE即可得.
解答 解:甲的做法如图所示: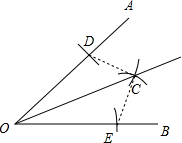
根据题意知,OD=OE,DC=EC,
在△ODC和△OEC中,
∵$\left\{\begin{array}{l}{OD=OE}\\{DC=EC}\\{OC=OC}\end{array}\right.$,
∴△ODC≌△OEC(SSS),
∴∠AOC=∠BOC,即OC为∠AOB的平分线;
乙的做法如图: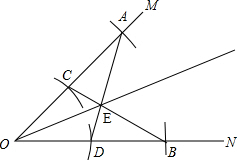
根据题意知:OA=OB、OD=OC,
∴AC=BD,
在△AOD和△BOC中,
∵$\left\{\begin{array}{l}{OA=OB}\\{∠AOD=∠BOC}\\{OD=OC}\end{array}\right.$,
∴△AOD≌△BOC(SAS),
∴∠OAD=∠OBC,
在△ACE和△BDE中,
∵$\left\{\begin{array}{l}{∠AEC=∠BED}\\{∠CAE=∠BDE}\\{AC=BD}\end{array}\right.$,
∴△ACE≌△BDE(AAS),
∴CE=DE,
在△OCE和△ODE中,
∵$\left\{\begin{array}{l}{OC=OD}\\{OE=OE}\\{CE=DE}\end{array}\right.$,
∴△OCE≌△ODE(SSS),
∴∠AOE=∠BOE,即OE为∠MON的平分线,
综上,甲、乙做法都对,
故选:D.
点评 本题主要考查基本作图及全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.

练习册系列答案
相关题目
6.已知函数y=-x2+6x-5,当x=m时,y>0,则m的取值可能是( )
| A. | -5 | B. | -1 | C. | $\frac{3}{2}$ | D. | 6 |
7.已知一个等腰三角形有两内角的度数之比为1:4,则这个等腰三角形顶角的度数为( )
| A. | 20° | B. | 120° | C. | 20°或120° | D. | 36° |
11.已知a>b,则下列不等式中,正确的是( )
| A. | -a>-b | B. | 3a<3b | C. | a+4>b+4 | D. | 2a-1>3b-1 |
1.下列语句中正确的是( )
| A. | 36的算术平方根是±6 | B. | -36的算术平方根是6 | ||
| C. | 36的平方根是-6 | D. | 36的算术平方报是6 |
8.用配方法方程x2+6x-5=0时,变形正确的方程为( )
| A. | (x+3)2=14 | B. | (x-3)2=14 | C. | (x+6)2=4 | D. | (x-6)2=4 |
 如图,菱形ABCD的对角线AC,BD交于点O,过点O作EF⊥AD,分别交AD,BC于点E,F,若AC=6,BD=8,则EF长为( )
如图,菱形ABCD的对角线AC,BD交于点O,过点O作EF⊥AD,分别交AD,BC于点E,F,若AC=6,BD=8,则EF长为( )