题目内容
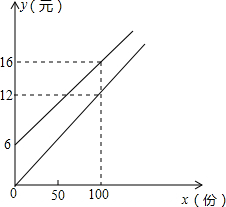 某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图:
某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图:(1)填空:甲种收费的函数表达式是
(2)该校某年级每次需印制320~350份学案,选择哪种印刷方式较合算?
考点:一次函数的应用
专题:
分析:(1)设出两种收费的函数表达式,代入图象上的点求得答案即可;
(2)由(1)的两个函数关系式,建立不等式,求得x的取值范围,进一步得出答案即可.
(2)由(1)的两个函数关系式,建立不等式,求得x的取值范围,进一步得出答案即可.
解答:解:(1)设甲种收费的函数表达式y1=kx+b,乙种收费的函数表达式是y2=k1x,
把(0,6),(100,16)代入y1=kx+b,得
,
解得
,
∴y1=0.1x+6(x≥0的整数),
把(100,12)代入y2=k1x,
解得:k1=0.12,
∴y2=0.12x(x≥0的整数);
∴y1=0.1x+6(x≥0的整数),y2=0.12x(x≥0的整数).
(2)由题意,得
当y1>y2时,0.1x+6>0.12x,得x<300;
当y1=y2时,0.1x+6=0.12x,得x=300;
当y1<y2时,0.1x+6<0.12x,得x>300;
∴当x在320~350范围时,选择甲种方式合算.
把(0,6),(100,16)代入y1=kx+b,得
|
解得
|
∴y1=0.1x+6(x≥0的整数),
把(100,12)代入y2=k1x,
解得:k1=0.12,
∴y2=0.12x(x≥0的整数);
∴y1=0.1x+6(x≥0的整数),y2=0.12x(x≥0的整数).
(2)由题意,得
当y1>y2时,0.1x+6>0.12x,得x<300;
当y1=y2时,0.1x+6=0.12x,得x=300;
当y1<y2时,0.1x+6<0.12x,得x>300;
∴当x在320~350范围时,选择甲种方式合算.
点评:此题考查待定系数法求函数解析式,以及一次函数与不等式的关系,结合图象,理解题意,解决问题.

练习册系列答案
相关题目
已知一次函数y=kx+b中,k<0,b<0,请问这函数不经过什么象限?( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图1,在⊙O中,E是
如图1,在⊙O中,E是
 如图,在△ABC和△ADE中,B、D、C三点在同一直线上.有以下四个条件:
如图,在△ABC和△ADE中,B、D、C三点在同一直线上.有以下四个条件:
 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD. 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.