题目内容
直角坐标系中,已知点P(1,1),在x轴上找一点A,使△AOP为等腰三角形,这样的点P共有 个.
考点:等腰三角形的判定,坐标与图形性质
专题:
分析:要使△AOP为等腰三角形,只需分两种情况考虑:OP当底边或OP当腰,当OP是底边时,则点A即为OP的垂直平分线和x轴的交点;当OP是腰时,则点A即为分别以O、P为圆心,以OP为半径的圆和x轴的交点(点O除外),从而得出答案.
解答: 解:(1)若AO作为腰时,有两种情况,当P是顶角顶点时,A是以P为圆心,以OP为半径的圆与x轴的交点,共有1个,
解:(1)若AO作为腰时,有两种情况,当P是顶角顶点时,A是以P为圆心,以OP为半径的圆与x轴的交点,共有1个,
当O是顶角顶点时,A是以O为圆心,以OP为半径的圆与x轴的交点,有2个;
(2)若OP是底边时,A是OP的中垂线与x轴的交点,有1个.
以上4个交点没有重合的.
故符合条件的点有4个.
故答案为:4.
 解:(1)若AO作为腰时,有两种情况,当P是顶角顶点时,A是以P为圆心,以OP为半径的圆与x轴的交点,共有1个,
解:(1)若AO作为腰时,有两种情况,当P是顶角顶点时,A是以P为圆心,以OP为半径的圆与x轴的交点,共有1个,当O是顶角顶点时,A是以O为圆心,以OP为半径的圆与x轴的交点,有2个;
(2)若OP是底边时,A是OP的中垂线与x轴的交点,有1个.
以上4个交点没有重合的.
故符合条件的点有4个.
故答案为:4.
点评:此题主要考查了坐标与图形的性质及等腰三角形的判定;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
下列命题中正确的是( )
| A、相似图形一定是位似图形 |
| B、若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积之比为3:4 |
| C、如果一条直线上有两点到另一条直线上的距离相等,那么这两条直线互相平行 |
| D、有一个内角是96°的两个等腰三角形相似 |
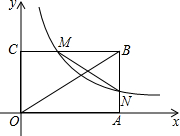 如图,点A在x轴正半轴上,点C在y正半轴上,四边形OABC为矩形,面积为6,双曲线y=
如图,点A在x轴正半轴上,点C在y正半轴上,四边形OABC为矩形,面积为6,双曲线y= 如图,在等腰△ABC中,AB=AC,BC边上的高AD=6cm,腰AB上的高CE=8cm,则△ABC的周长等于
如图,在等腰△ABC中,AB=AC,BC边上的高AD=6cm,腰AB上的高CE=8cm,则△ABC的周长等于
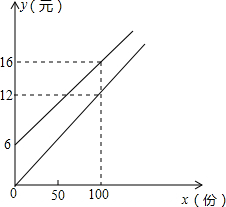 某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图:
某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图: