题目内容
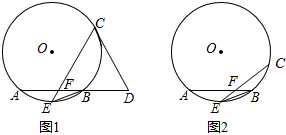 如图1,在⊙O中,E是
如图1,在⊙O中,E是 |
| AB |
| 2 |
| 3 |
(1)D为AB延长线上一点,若DC=DF,证明:直线DC与⊙O相切;
(2)求EF•EC的值;
(3)如图2,当F是AB的四等分点时,求EC的值.
考点:圆的综合题,勾股定理的应用,垂径定理,圆周角定理,切线的判定,相似三角形的应用
专题:几何综合题
分析:(1)连接OC、OE,OE交AB于H,如图1,由E是
的中点,根据垂径定理的推论得到OE⊥AB,则∠HEF+∠HFE=90°,由对顶相等得∠HFE=∠CFD,则∠HEF+∠CFD=90°,再由DC=DF得∠CFD=∠DCF,加上∠OCE=∠OEC,所以∠OCE+∠DCE=∠HEF+∠CFD=90°,于是根据切线的判定定理得直线DC与⊙O相切;
(2)由
=
,根据圆周角定理得到∠ABE=∠BCE,加上∠FEB=∠BEC,于是可判断△EBF∽△ECB,利用相似比得到EF•EC=BE2=(
r)2=
r2;
(3)如图2,连接OA,由
=
得AE=BE=
r,设OH=x,则HE=r-x,根据勾股定理,在Rt△OAH中有AH2+x2=r2;在Rt△EAH中由AH2+(r-x)2=(
r)2,利用等式的性质得x2-(r-x)2=r2-(
r)2,即得x=
r,则HE=r-
r=
r,在Rt△OAH中,根据勾股定理计算出AH=
,由OE⊥AB得AH=BH,而F是AB的四等分点,所以HF=
AH=
,于是在Rt△EFH中可计算出EF=
r,然后利用(2)中的结论可计算出EC.
 |
| AB |
(2)由
 |
| AE |
 |
| BE |
| 2 |
| 3 |
| 4 |
| 9 |
(3)如图2,连接OA,由
 |
| AE |
 |
| BE |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 7 |
| 9 |
| 7 |
| 9 |
| 2 |
| 9 |
4
| ||
| 9 |
| 1 |
| 2 |
2
| ||
| 9 |
2
| ||
| 9 |
解答: (1)证明:连接OC、OE,OE交AB于H,如图1,
(1)证明:连接OC、OE,OE交AB于H,如图1,
∵E是
的中点,
∴OE⊥AB,
∴∠EHF=90°,
∴∠HEF+∠HFE=90°,
而∠HFE=∠CFD,
∴∠HEF+∠CFD=90°,
∵DC=DF,
∴∠CFD=∠DCF,
而OC=OE,
∴∠OCE=∠OEC,
∴∠OCE+∠DCE=∠HEF+∠CFD=90°,
∴OC⊥CD,
∴直线DC与⊙O相切;
(2)解:连接BC,
∵E是
的中点,
∴
=
,
∴∠ABE=∠BCE,
而∠FEB=∠BEC,
∴△EBF∽△ECB,
∴EF:BE=BE:EC,
∴EF•EC=BE2=(
r)2=
r2;
(3)解:如图2,连接OA,
∵
=
,
∴AE=BE=
r,
设OH=x,则HE=r-x,
在Rt△OAH中,AH2+OH2=OA2,即AH2+x2=r2,
在Rt△EAH中,AH2+EH2=EA2,即AH2+(r-x)2=(
r)2,
∴x2-(r-x)2=r2-(
r)2,即得x=
r,
∴HE=r-
r=
r,
在Rt△OAH中,AH=
=
=
,
∵OE⊥AB,
∴AH=BH,
而F是AB的四等分点,
∴HF=
AH=
,
在Rt△EFH中,EF=
=
=
r,
∵EF•EC=
r2,
∴
r•EC=
r2,
∴EC=
r.
 (1)证明:连接OC、OE,OE交AB于H,如图1,
(1)证明:连接OC、OE,OE交AB于H,如图1,∵E是
 |
| AB |
∴OE⊥AB,
∴∠EHF=90°,
∴∠HEF+∠HFE=90°,
而∠HFE=∠CFD,
∴∠HEF+∠CFD=90°,
∵DC=DF,
∴∠CFD=∠DCF,
而OC=OE,
∴∠OCE=∠OEC,
∴∠OCE+∠DCE=∠HEF+∠CFD=90°,
∴OC⊥CD,
∴直线DC与⊙O相切;
(2)解:连接BC,
∵E是
 |
| AB |
∴
 |
| AE |
 |
| BE |
∴∠ABE=∠BCE,
而∠FEB=∠BEC,
∴△EBF∽△ECB,
∴EF:BE=BE:EC,
∴EF•EC=BE2=(
| 2 |
| 3 |
| 4 |
| 9 |
(3)解:如图2,连接OA,

∵
 |
| AE |
 |
| BE |
∴AE=BE=
| 2 |
| 3 |
设OH=x,则HE=r-x,
在Rt△OAH中,AH2+OH2=OA2,即AH2+x2=r2,
在Rt△EAH中,AH2+EH2=EA2,即AH2+(r-x)2=(
| 2 |
| 3 |
∴x2-(r-x)2=r2-(
| 2 |
| 3 |
| 7 |
| 9 |
∴HE=r-
| 7 |
| 9 |
| 2 |
| 9 |
在Rt△OAH中,AH=
| OA2-OH2 |
r2-(
|
4
| ||
| 9 |
∵OE⊥AB,
∴AH=BH,
而F是AB的四等分点,
∴HF=
| 1 |
| 2 |
2
| ||
| 9 |
在Rt△EFH中,EF=
| HE2+HF2 |
(
|
2
| ||
| 9 |
∵EF•EC=
| 4 |
| 9 |
∴
2
| ||
| 9 |
| 4 |
| 9 |
∴EC=
2
| ||
| 3 |
点评:本题考查了圆的综合题:熟练掌握垂径定理及其推论、切线的判定定理和圆周角定理;会利用勾股定理进行几何计算,利用相似三角形的知识解决有关线段等积的问题.

练习册系列答案
相关题目
下列命题中正确的是( )
| A、相似图形一定是位似图形 |
| B、若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积之比为3:4 |
| C、如果一条直线上有两点到另一条直线上的距离相等,那么这两条直线互相平行 |
| D、有一个内角是96°的两个等腰三角形相似 |
这次万菁初中有21参加拔尖人才考试,考试成绩各不相同,假设这次考试只取前10名,小峰同学已经知道自己的成绩,他想知道自己能否被录取,他还需要知道其他20名同学成绩的( )
| A、众数 | B、平均数 |
| C、中位数 | D、极差 |
已知抛物线y=-x2+6x+m上有三点:A(1,y1)、B(2,y2)、C(3+
,y3),则y1、y2、y3的大小关系是( )
| 2 |
| A、y2<y1<y3 |
| B、y1<y2<y3 |
| C、y1<y3<y2 |
| D、y3<y1<y2 |
 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).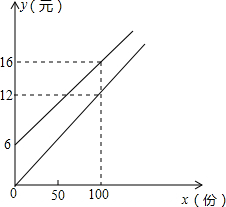 某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图:
某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图:
 二次函数图象的顶点在原点O,经过点A(1,
二次函数图象的顶点在原点O,经过点A(1,