题目内容
2.有长度为3cm,5cm,7cm,9cm的四条线段,从中任取三条线段,能够组成三角形的概率是$\frac{3}{4}$.分析 由四条线段中任意取3条,是一个列举法求概率问题,是无放回的问题,共有4种可能结果,每种结果出现的机会相同,满足两边之和大于第三边构成三角形的有3个结果.因而就可以求出概率.
解答 解:由四条线段中任意取3条,共有4种可能结果,每种结果出现的机会相同,满足两边之和大于第三边构成三角形的有3个结果,所以P(取出三条能构成三角形)=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 考查了概率的求法即三角形的三边关系,用到的知识点为:概率等于所求情况数与总情况数之比;组成三角形的两条小边之和大于最大的边.

练习册系列答案
相关题目
7.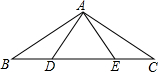 如图,点D、E在△ABC的BC边上,∠BAD=∠CAE,再添加一个条件能推理得出△ABE≌△ACD,(不添加辅助线),下列条件不可以的是( )
如图,点D、E在△ABC的BC边上,∠BAD=∠CAE,再添加一个条件能推理得出△ABE≌△ACD,(不添加辅助线),下列条件不可以的是( )
 如图,点D、E在△ABC的BC边上,∠BAD=∠CAE,再添加一个条件能推理得出△ABE≌△ACD,(不添加辅助线),下列条件不可以的是( )
如图,点D、E在△ABC的BC边上,∠BAD=∠CAE,再添加一个条件能推理得出△ABE≌△ACD,(不添加辅助线),下列条件不可以的是( )| A. | ∠B=∠C | B. | AB=AC | C. | ∠ADE=∠AED | D. | ∠B=∠CAE |
11.在Rt△ABC中,∠C=90°,a=1,c=4,则tanA的值是( )
| A. | $\frac{\sqrt{15}}{15}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{15}}{4}$ |
12.若25x2+30xy+k是一个完全平方式,则k是( )
| A. | 36y2 | B. | 9y2 | C. | 6y2 | D. | y2 |