题目内容
19．如图中，图1图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．在Rt△ABC中，若直角边AC=6，BC=5，将四个直角三角形中边长为6的直角边向外延长一倍，得到图2所示的“数学风车”，则这个风车外围周长（图2中的实线）是76．
分析 由题意∠ACB为直角，利用勾股定理求得外围中一条边，又由AC延伸一倍，从而求得风车的一个轮子，进一步求得四个．
解答 解：依题意，设“数学风车”中的四个直角三角形的斜边长为x，则
x2=122+52=169，
所以x=13．
所以“数学风车”的周长是：（13+6）×4=76．
故答案为：76．
点评 本题考查了勾股定理在实际情况中应用，并注意隐含的已知条件来解答此类题．
练习册系列答案
相关题目
如图，在△ABC中，D是AB的中点，F是BC边延长线上的点，连结DF交AC于点E．求证：CF：BF=CE：AE．（提示：过点C作CG∥AB）
7．
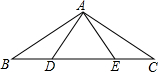如图，点D、E在△ABC的BC边上，∠BAD=∠CAE，再添加一个条件能推理得出△ABE≌△ACD，（不添加辅助线），下列条件不可以的是（ ）
如图，点D、E在△ABC的BC边上，∠BAD=∠CAE，再添加一个条件能推理得出△ABE≌△ACD，（不添加辅助线），下列条件不可以的是（ ）| A． | ∠B=∠C | B． | AB=AC | C． | ∠ADE=∠AED | D． | ∠B=∠CAE |
4．由$\frac{a}{b}$=$\frac{3}{5}$，不能推出的比例式是（ ）
| A． | $\frac{a}{3}$=$\frac{b}{5}$ | B． | $\frac{a+b}{b}$=$\frac{8}{5}$ | C． | $\frac{b-a}{a}$=$\frac{3}{2}$ | D． | $\frac{a+3}{b+5}$=$\frac{3}{5}$（b+5≠0） |
11．在Rt△ABC中，∠C=90°，a=1，c=4，则tanA的值是（ ）
| A． | $\frac{\sqrt{15}}{15}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{\sqrt{15}}{4}$ |