题目内容
19.若关于x的方程x2-mx+m=0有两个相等实数根,则代数式2m2-8m+1的值为1.分析 根据方程的系数结合根的判别式即可得出△=m2-4m=0,将其代入2m2-8m+1中即可得出结论.
解答 解:∵关于x的方程x2-mx+m=0有两个相等实数根,
∴△=(-m)2-4m=m2-4m=0,
∴2m2-8m+1=2(m2-4m)+1=1.
故答案为:1.
点评 本题考查了根的判别式,熟练掌握“当△=0时,方程有两个相等的两个实数根”是解题的关键.

练习册系列答案
相关题目
9.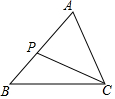 如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )
如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )
 如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )
如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{AC}{AB}=\frac{CP}{BC}$ | D. | $\frac{AC}{AP}=\frac{AB}{AC}$ |
10.设三角形三边之长分别为3,8,1-2a,则a的取值范围为( )
| A. | -6<a<-3 | B. | -5<a<-2 | C. | -2<a<5 | D. | a<-5或a>2 |
8.整理一批图书,由一个人做要40h完成,现计划有一部分人先做4h,然后增加2人与他们一起做8h,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人工作?如果设安排x人先做4h,下列四个方程中正确的是( )
| A. | $\frac{4(x+2)}{40}$+$\frac{8x}{40}$=1 | B. | $\frac{4x}{40}$+$\frac{8(x+2)}{40}$=1 | C. | $\frac{4x}{40}$+$\frac{8(x-2)}{40}$=1 | D. | $\frac{4(x-2)}{40}$+$\frac{8x}{40}$=1 |
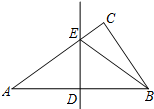 如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=5,AC=4,则△BCE的周长是7.
如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=5,AC=4,则△BCE的周长是7.