题目内容
19. 如图,在△ABC中,点D,E分别在AB,AC上,∠AED=∠ABC.
如图,在△ABC中,点D,E分别在AB,AC上,∠AED=∠ABC.(1)求证:△ADE∽△ACB;
(2)若AD=2,AE=3,AC=6,求AB的长.
分析 (1)根据已知∠AED=∠ABC,∠A=∠A,进而得出△ADE∽△ACB;
(2)利用相似三角形的性质解答即可.
解答 证明:(1)∵∠AED=∠ABC,∠A=∠A
∴△ADE∽△ACB
(2)∵△ADE∽△ACB
∴$\frac{AD}{AC}=\frac{AC}{AB}$即 $\frac{2}{6}=\frac{3}{AB}$,
∴AB=9.
点评 此题主要考查了相似三角形的判定和性质,熟练掌握相似三角形的判定方法是解题关键.

练习册系列答案
相关题目
10.某型号的手机连续两次降价,每个售价由原来的1225元降到了625元,设平均每次降价的百分率为x,列出方程正确的是( )
| A. | 625(1+x)2=1225 | B. | 1225(1+x)2=625 | C. | 625(1-x)2=1225 | D. | 1225(1-x)2=625 |
14.若(x-1)2+$\sqrt{x+y}$=0,则x2016+y2017的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
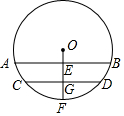 如图,圆柱形水管内原有积水的水平面宽CD=10cm,水深GF=1cm,若水面上升1cm(EG=1cm),则此时水面宽AB为多少?
如图,圆柱形水管内原有积水的水平面宽CD=10cm,水深GF=1cm,若水面上升1cm(EG=1cm),则此时水面宽AB为多少?