题目内容
8.计算题(1)2$\sqrt{12}$+3$\sqrt{1\frac{1}{3}}$-$\sqrt{5\frac{1}{3}}$-$\frac{2}{3}$$\sqrt{48}$
(2)(2-$\sqrt{3}$)2013(2+$\sqrt{3}$)2014-2|-$\frac{\sqrt{3}}{2}$|-(-$\sqrt{3}$)0
(3)$\sqrt{\frac{12}{x}}$?$\frac{1}{2}$$\sqrt{\frac{3}{xy}}$÷(-$\frac{3}{4}$$\sqrt{\frac{18}{x{y}^{2}}}$)
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)根据积的乘方和零指数幂的意义得到原式=[(2-$\sqrt{3}$)(2+$\sqrt{3}$)]2013•(2+$\sqrt{3}$)-2×$\frac{\sqrt{3}}{2}$-1,然后利用平方差公式计算后合并即可;
(3)根据二次根式的乘除法则运算.
解答 解:(1)原式=4$\sqrt{3}$+2$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$-$\frac{8\sqrt{3}}{3}$
=0;
(2)原式=[(2-$\sqrt{3}$)(2+$\sqrt{3}$)]2013•(2+$\sqrt{3}$)-2×$\frac{\sqrt{3}}{2}$-1
=(4-3)2013•(2+$\sqrt{3}$)-$\sqrt{3}$-1
=2+$\sqrt{3}$-$\sqrt{3}$-1
=1;
(3)原式=$\frac{1}{2}$•(-$\frac{4}{3}$)•$\sqrt{\frac{12}{x}•\frac{3}{xy}•\frac{x{y}^{2}}{18}}$
=-$\frac{2\sqrt{2xy}}{3x}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
18.下列所示的图案中,有且仅有一条对称轴的是( )
| A. |  | B. |  | C. |  | D. |  |
19.下列说法中正确的是( )
| A. | 一个角的补角一定大于这个角 | B. | 锐角的补角一定是钝角 | ||
| C. | 直角的补角可能是锐角或钝角 | D. | 锐角和钝角互补 |
20.下列各式正确的是( )
| A. | x2•x3=x6 | B. | (xn+1)2=x2n+1 | C. | (-2xy2)2=4x2y4 | D. | 2x+x=2x2 |
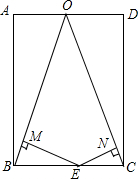 如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB,OC,点E在线段BC上(点E不与B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为$\frac{3\sqrt{10}}{5}$.
如图,在矩形ABCD中,AB=3,BC=2,O是AD的中点,连接OB,OC,点E在线段BC上(点E不与B、C重合),过点E作EM⊥OB于M,EN⊥OC于N,则EM+EN的值为$\frac{3\sqrt{10}}{5}$.