题目内容
14.某校初三(1)班进行立定跳远训练,以下是李超和陈辉同学六次的训练成绩(单位:m)| 1 | 2 | 3 | 4 | 5 | 6 | |
| 李超 | 2.50 | 2.42 | 2.52 | 2.56 | 2.48 | 2.58 |
| 陈辉 | 2.54 | 2.48 | 2.50 | 2.48 | 2.54 | 2.52 |
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?
分析 (1)分别求出6个数的和再除以6即可;
(2)利用方差公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],分别进行计算;
(3)数一数两人谁能跳过2.55米的次数多即可.
解答 解:(1)李超的平均成绩:(2.50+2.42+2.52+2.56+2.48+2.58)÷6=2.51,
陈辉的平均成绩:(2.54+2.48+2.50+2.48+2.54+2.52)÷6=2.51;
(2)李超:S2=$\frac{1}{6}$[(2.50-2.51)2+(2.42-2.51)2+(2.52-2.51)2+(2.56-2.51)2+(2.48-2.51)2+(2.58-2.51)2]=2.77×10-3,
陈辉:S2=$\frac{1}{6}$[(2.54-2.51)2+(2.48-2.51)2+(2.50-2.51)2+(2.48-2.51)2+(2.54-2.51)2+(2.52-2.51)2]≈6.33×10-4,
陈辉的成绩稳定,因为他的方差小.
(3)选李超,因为他能跳过2.55米的可能性大.
点评 此题主要考查了平均数和方差,关键是掌握方差公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.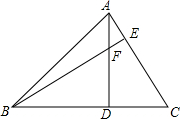 如图,已知AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,DF=DC,则∠ABC的大小是( )
如图,已知AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,DF=DC,则∠ABC的大小是( )
 如图,已知AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,DF=DC,则∠ABC的大小是( )
如图,已知AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,DF=DC,则∠ABC的大小是( )| A. | 30度 | B. | 45度 | C. | 60度 | D. | 无法确定 |
2.化简($\sqrt{3}$-2)2015•($\sqrt{3}$+2)2016的结果为( )
| A. | -1 | B. | $\sqrt{3}$-2 | C. | $\sqrt{3}$+2 | D. | -$\sqrt{3}$-2 |