题目内容
16.已知方程组$\left\{\begin{array}{l}{2a-3b=7}\\{3a+5b=1}\end{array}\right.$的解为$\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$,则方程组$\left\{\begin{array}{l}{2(x-3)-3(y+2)=7}\\{3(x-3)+5(y+2)=1}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=5}\\{y=-3}\end{array}\right.$.分析 根据题意可得方程组$\left\{\begin{array}{l}{x-3=2}\\{y+2=-1}\end{array}\right.$,解方程组即可求解.
解答 解:依题意有
$\left\{\begin{array}{l}{x-3=2}\\{y+2=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=5}\\{y=-3}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x=5}\\{y=-3}\end{array}\right.$.
点评 此题主要考查了二元一次方程组的解,关键是根据题意得到方程组$\left\{\begin{array}{l}{x-3=2}\\{y+2=-1}\end{array}\right.$.

练习册系列答案
相关题目
4.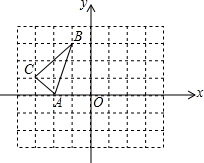 如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(-2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )
如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(-2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )
 如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(-2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )
如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(-2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )| A. | (1,-1) | B. | (1,1) | C. | (-1,1) | D. | (-1,-1) |
1.向量($\overrightarrow{AB}$+$\overrightarrow{MB}$)+($\overrightarrow{BO}$+$\overrightarrow{BC}$)+$\overrightarrow{OM}$化简后的结果等于( )
| A. | $\overrightarrow{BC}$ | B. | $\overrightarrow{AB}$ | C. | $\overrightarrow{AC}$ | D. | $\overrightarrow{AM}$ |
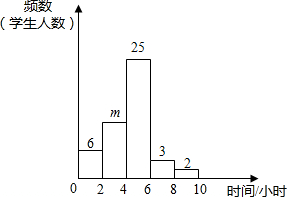 分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题: