题目内容
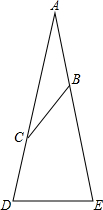 如图,在△ABC中,已知:AB=BC=CD=DE,∠A=20°,求∠E的度数.
如图,在△ABC中,已知:AB=BC=CD=DE,∠A=20°,求∠E的度数.考点:等腰三角形的性质
专题:
分析:以点C为圆心,以线段CB为半径画弧,与AE交于F,连接CF,连接DF,在△ABC和△CBF中利用外角及三角形内角和定理求出∠DCF,再结合等腰三角形的性质,可求得∠DFE=∠E=80°.
解答: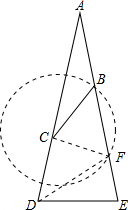
解:以点C为圆心,以线段CB为半径画弧,与AE交于F,连接CF,连接DF,
∴CF=CB,
∵AB=CB,∠A=20°,
∴∠CBF=CFB=40°,
∴∠BCF=100°,∠DCF=(180-20-100)°=60°,
∵CF=CB=CD,
∴CF=CD,∠DCF=60°,
∴∠CDF=∠CFD=60°,
∴DF=CD,
∴∠DFE=(180-40-60)°=80°,
∵DF=CD,CD=DE,
∴DF=DE,
∴∠E=∠DFE=80°.

解:以点C为圆心,以线段CB为半径画弧,与AE交于F,连接CF,连接DF,
∴CF=CB,
∵AB=CB,∠A=20°,
∴∠CBF=CFB=40°,
∴∠BCF=100°,∠DCF=(180-20-100)°=60°,
∵CF=CB=CD,
∴CF=CD,∠DCF=60°,
∴∠CDF=∠CFD=60°,
∴DF=CD,
∴∠DFE=(180-40-60)°=80°,
∵DF=CD,CD=DE,
∴DF=DE,
∴∠E=∠DFE=80°.
点评:本题主要考查等腰三角形的性质及三角形内角和定理、外角的性质,以点C为圆心,以线段CB为半径画弧构造出等腰三角形是解题的关键.

练习册系列答案
相关题目
下列方程中,是一元二次方程的是( )
| A、x+3=0 | ||
| B、x2-3y=0 | ||
| C、(x+3)(x-3)=1 | ||
D、x-
|
 如图所示,C是⊙O上一点,O是圆心,若∠AOB=80°,则∠ACB=( )
如图所示,C是⊙O上一点,O是圆心,若∠AOB=80°,则∠ACB=( )| A、20° | B、30° |
| C、40° | D、50° |
下列说法中,正确的是( )
| A、算术平方根等于它本身的数只有0 |
| B、平方根等于它本身的数有0,±1 |
| C、立方根等于它本身的数有±1 |
| D、无论是有理数还是无理数,都可以用数轴上的点来表示 |
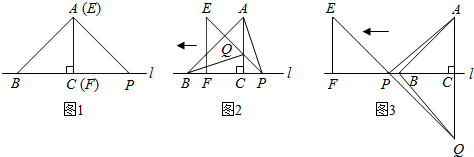
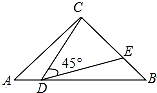 如图,△ABC中,∠ACB=90°,AC=BC=2,点D在线段AB上运动(不包括端点),∠CDE=45°,DE与CB交于点E,若DB=x,CE=y.
如图,△ABC中,∠ACB=90°,AC=BC=2,点D在线段AB上运动(不包括端点),∠CDE=45°,DE与CB交于点E,若DB=x,CE=y.